Последовательность работы генетического алгоритма

Общая схема работы генетического алгоритма представлена на рис. 9.1.

Формирование исходной популяции происходит с исполь­зованием какого-либо случайного закона, на основе которого выбирается нужное количество точек поискового пространства. Исходная популяция может также быть результатом работы какого-либо другого алгоритма оптимизации.

В основе оператора отбора, который служит для выбора родительских пар и уничтожения особей, лежит принцип “выживает сильнейший”. В ка­честве примера можно привести следующий оператор. Выбор особи для размножения производится случайно. Вероятность участия особи в про­цессе размножения вычисляется по формуле:

,

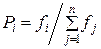где Р_i – вероятность участия особи в процессе размножения, i – номер осо­би,

п – размер популяции, f_i – значение целевой функции для i-ой особи. В данном случае целью поиска является нахождение максимума целевой фун­кции. Одна особь может быть задействована в нескольких родительских парах.

Рис. 9.1 Процесс работы генетического алгоритма

Аналогично может быть решен вопрос уничтожения особей. Только вероятность уничтожения, соответственно, должна быть обратно пропор­циональна качеству особей. Однако обычно просто уничто­жают особей с наихудшим качеством. Таким образом, выбирая для раз­множения наиболее качественные особи и уничтожая наиболее слабые, генетический алгоритм постоянно улучшает популяцию, приводя к фор­мированию лучших решений.

Оператор скрещивания призван моделировать природный процесс наследования, т. е. обеспечивать передачу свойств родителей потомкам.

Рассмотрим простейший оператор скрещивания. Он выполняется в два этапа. Пусть особь представляет собой строку из тэлементов. На первом этапе равновероятно выбирается натуральное число k от 1 до m–1. Это число называется точкой разбиения. В соответствии с ним обе исходные строки разбиваются на две подстроки. На втором этапе строки обменива­ются своими подстроками, лежащими после точки разбиения, то есть эле­ментами с k+1-го по m-й. Так получаются две новые строки, которые наследовали частично свойства обоих родителей. Этот процесс проиллюст­рирован ниже.

Строка1 X₁X₂ . . . X_k X_k+1 . . . X_m X₁ X₂ . . . X_k Y_k+1 . . . Y_m

Строка2 Y₁ Y₂ . . . Y_k Y_k+1 . . . Y_m Y₁ Y₂ . . . Y_k X_k+1 . . . X_m

Вероятность применения оператора скрещивания обычно выбирается достаточно большой, в пределах от 0,9 до 1, чтобы обеспечить постоянное появление новых особей, расширяющих пространство поиска.

Оператор мутации служит для моделирования природного процесса мутации. Его применение в генетических алгоритмах обусловлено следу­ющими соображениями. Исходная популяция, какой бы большой она ни была, охватывает ограниченную область пространства поиска. Оператор скрещивания, безусловно, расширяет эту область, но все же до определен­ной степени, поскольку использует ограниченный набор значений, задан­ный исходной популяцией. Внесение случайных изменений в особи позво­ляет преодолеть это ограничение и иногда значительно сократить время поиска и улучшить качество результата.

Как правило, вероятность мутации, в отличие от вероятности скрещи­вания, выбирается достаточно малой. Сам процесс мутации заключается в замене одного из элементов строки на другое значение. Это может быть перестановка двух элементов в строке, замена элемента строки значением элемента из другой строки, в случае битовой строки может применяться инверсия одного из битов и т. д.

В процессе работы алгоритма все указанные выше операторы приме­няются многократно и ведут к постепенному изменению исходной популя­ции. Поскольку операторы отбора, скрещивания, мутации и редукции по своей сути направлены на улучшение каждой отдельной особи, то резуль­татом их работы является постепенное улучшение популяции в целом.

После завершения работы генетического алгоритма из конечной попу­ляции выбирается та особь, которая дает экстремальное (максимальное или минимальное) значение целевой функции и является, таким образом, результатом работы генетического алгоритма. За счет того, что конечная популяция лучше исходной, полученный результат представляет собой улучшенное решение.