Алгоритм перебора в глубину

Определим глубину вершины числом, равным номеру ее уровня. При переборе в глубину всегда раскрывается вершина, имеющая наибольшую глубину. По тем или иным соображениям задается граничная глубина. Вершины, имеющие глубину, равную граничной, не раскрываются. Таким образом, метод перебора в глубину можно определить как метод перебора, при котором всегда раскрывается та из вершин, которая имеет наибольшую глубину, меньшую граничной.

Алгоритм перебора в глубину включает следующие шаги.

1. Поместить начальную вершину в список ОТК.

2. Если список ОТК пуст, выдать сообщение о неудаче поиска, иначе перейти к шагу 3.

3. Взять первую вершину из списка ОТК и поместить в список ЗКР. Присвоить этой вершине идентификатор .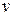

4. Если глубина вершины 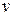равна граничной глубине, то перейти к шагу 2, иначе – к шагу 5.

5. Раскрыть вершину 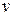. Поместить все дочерние вершины в начало списка ОТК и построить указатели, идущие от них к вершине 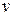. Если 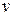не имеет дочерних вершин, то перейти к шагу 2.

6. Если одна из этих вершин целевая, то выдать решение, в ином случае перейти к шагу 2.

Один из возможных графов решения задачи выбора маршрута с помощью алгоритма перебора в глубину приведен на рис. 8.5. При применении этого алгоритма решение зависит от способа упорядочения вершин в списке ОТК. В приведенном решении найден неоптимальный маршрут.

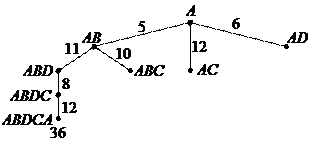Рис. 8.5 Граф решения задачи о выборе маршрута при использовании алгоритма перебора в глубину

Во всех рассмотренных алгоритмах перебора предполагается, что начальная вершина только одна. Если начальных вершин несколько, то эти алгоритмы изменяются только на шаге 1: на шаге 1 в список ОТК помещаются все начальные вершины.

Достоинством методов слепого перебора являются, во-первых, простота алгоритмической реализации, во-вторых, обязательность получения решения, если оно существует. Недостатком этих методов является резкое возрастание числа вершин, которые необходимо раскрыть в процессе поиска решения, с увеличением размерности задачи. Это существенно сужает круг практических задач, которые могут быть решены методами слепого перебора.