Поиск решений в пространстве состояний

Поиск решений в пространстве состояний сводится к определению последовательности операторов, отображающих начальные состояния в целевые. Если такая последовательность не одна и задан критерий оптимальности, то поиск сводится к нахождению оптимальной последовательности, т.е. последовательности операторов, обеспечивающей экстремум заданного критерия оптимальности. Для поиска решений в пространстве состояний удобно использовать дерево (граф) состояний. На дереве состояний поиск решения сводится к определению пути (оптимального, если задан критерий оптимальности) от корня дерева к целевой вершине. Наглядно поиск можно проиллюстрировать на дереве состояний, когда начальное состояние одно. Поэтому сначала рассмотрим задачи, определяемые тройкой (S₀, F, G), где множество S₀ начальных состояний состоит из одного элемента. В указанной тройке F-множество операторов, G – множество целевых состояний.

Для построения дерева состояний следует, используя операторы из множества F, применимые к начальному состоянию (корню дерева), построить вершины первого уровня. Затем используя, операторы из F, применимые к вершинам первого уровня, построить вершины второго уровня и т.д. Применение операторов к какой-либо вершине дерева для построения всех ее дочерних вершин называется раскрытием вершины, поэтому операторы из множества F рассматриваются как правила раскрытия вершин. После порождения дочерних вершин производится проверка, не являются ли они целевыми. Если целевая вершина не обнаружена, то выполняется следующий этап раскрытия путем применения правил раскрытия к каждой вершине, порожденной на предыдущем этапе. Полученное множество вершин вновь анализируется на присутствие целевой вершины. Процесс продолжается до обнаружения целевой вершины.

Рассмотрим процедуру построения графа состояний на примере выбора маршрута транспортным роботом. Схема маршрутов представлена на рис. 8.1.

А – начальный пункт. Состояние обозначается строкой, в которой перечисляются все пункты, пройденные к текущему моменту. Операторы соответствуют выбору того или иного маршрута. Так как из каждого пункта можно попасть в любые другие 3 пункта, то множество состоит из 12 операторов, причем применимыми к любому данному состоянию являются не более трех операторов.

На графе состояний этой задачи (рис. 8.3) начальной вершине (корню дерева) соответствует состояние А. Корень дерева порождает три дочерние вершины, соответствующие состояниям AB, AC и AD. Каждая из вершин, порожденных корнем, порождает по две вершины и каждая из вершин второго и третьего уровней – по одной. На дугах указаны расстояния, которые проходит робот при переходе из одного состояния в другое. На концевых вершинах, соответствующих целевым состояниям, указаны также длины маршрутов из начального состояния в целевое.

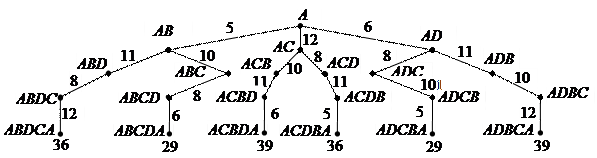
Рис. 8.3 Граф состояний задачи о выборе маршрута

Поиск решений имеет итеративный характер, причем число итераций и вершин, раскрытых до нахождения целевой вершины, существенно зависит от порядка раскрытия вершин. Порядок раскрытия вершин называют стратегией поиска.

Выделяют два основных типа стратегий поиска: «слепой» перебор и упорядоченный перебор вершин – кандидатов на раскрытие. Слепой перебор характеризуется тем, что расположение целевых вершин или их близость не влияют на порядок раскрытия. Существует несколько алгоритмов слепого перебора. Рассмотрим три наиболее типичных: алгоритм полного перебора, алгоритм равных цен, алгоритм перебора в глубину.