Представление, сводящее задачу к подзадачам

Такое представление предусматривает разбиение исходной задачи на множество подзадач, раздельное решение которых дает решение исходной задачи. Каждая из подзадач может в свою очередь также разбиваться на подзадачи. Разбиение продолжается до получения на нижнем уровне множества подзадач, способ решения которых известен. Такие задачи называются элементарными.

Существует два типа структур взаимосвязи подзадач: И – структуры и И/ИЛИ – структуры. В И – структурах для решения основной задачи требуется решить все подзадачи. В И/ИЛИ – структурах подзадачи разбиваются на группы, внутри которых они связанны отношением И, а между группами – отношением ИЛИ. В этом случае для решения исходной задачи достаточно решить все подзадачи какой-либо одной группы.

Для описания представления путем сведения задач к подзадачам используют граф, называемый И/ИЛИ графом. Вершинам графа соответствуют задачи, а дугам – операторам разбиения задач. Причем корню графа соответствует исходная задача, вершинам первого уровня – задачи, непосредственно порожденные исходной задачей, вершинам второго уровня – задачи, порожденные задачами первого уровня, и т.д.

Предположим, что задача A может быть решена, если будут решены задачи B и C или задача D; задача B будет решена, если решены задачи E или F; задача C – если решена G; задача D – если решены H и I. Граф такого представления задачи А приведен на рис. 8.2.

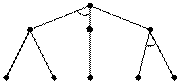A

B C D

E F G H I

Рис. 8.2 И/ИЛИ–граф для задачи А

Для обозначения вершин, связанных отношением И, на графе дуги, входящие в эти вершины, соединяются перемычками (в примере связаны вершины В и С, Н и I).

Структурно И/ИЛИ – граф отличается от графа состояния наличием связанных вершин, которые также называются И–вершинами, а несвязанные вершины – ИЛИ–вершинами. Вершины, соответствующие элементарным задачам, называются заключительными или терминальными вершинами. Вершины, не имеющие дочерних вершин и не являющиеся заключительными, называются тупиковыми. Тупиковым вершинам соответствуют задачи, которые в рамках данного представления не разрешимы. Разрешимой вершине соответствует разрешимая задача. Вершина, не являющаяся ни тупиковой, ни заключительной, будет разрешимой, когда все ее дочерние вершины разрешимы, если они являются связанными, или хотя бы одна из дочерних вершин разрешима, если они являются несвязанными. Задача А (рис. 8.2) разрешима, если вершины H и I являются заключительными, или заключительными являются вершины Е и G или F и G.