Понятие искусственного нейрона

Искусственный нейрон имитирует приближенно свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рис. 10.1 представлена модель, реализующая эту идею. Здесь множество входных сигналов 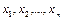в совокупности обознены вектором Х. Каждый сигнал умножается на соответствующий вес 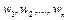и поступает в суммирующий блок, обозначенный 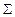. Множество весов в совокупности обозначают вектором W. Суммирующий блок, соответствующий телу биологического нейрона, складывает взвешенные входы алгебраически, создавая выход NET. В векторных обозначениях это можно записать следующим образом:

.

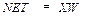Сигнал NET далее преобразуется активационной функцией F и дает выходной сигнал нейрона OUT (см. рис.10.2).

Рис. 10.2 Искусственный нейрон с активационной функцией

Активационная функция может быть линейной функцией

,

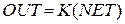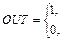
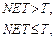
где T – некоторая постоянная пороговая величина.

В качестве активационной функции может также использоваться нелинейная функция, более точно моделирующая нелинейную передаточную характеристику биологического нейрона.

Если активационная функция сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется сжимающей функцией. В качестве сжимающей функции часто используется логистическая или сигмоидальная (S –

образная) функция 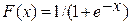, показанная на рис.10.3. Таким образом,

.

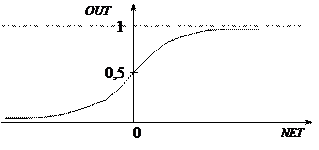
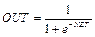Рис. 10.3 Логистическая функция

Активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления равен отношению приращения величины OUT к вызвавшему его небольшому приращению величины NET. Коэффициент усиления выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Нейрон с такой функцией может обрабатывать как слабые сигналы, которые он усиливает, так и сильные, которые усиливать не нужно.

Другой широко используемой нелинейной активационной функцией является гиперболический тангенс (см. рис. 10.4). В качестве активационной функции искусственного нейрона она записывается следующим образом:

,

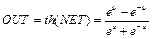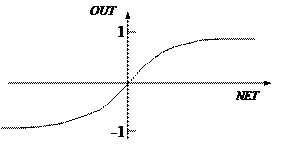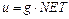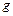где ; – приращение. Например, 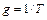(Т – пороговое значение).

Рис. 10.4 Функция гиперболического тангенса

Подобно логистической функции гиперболический тангенс является S – образной функцией, но он симметричен относительно начала координат и в точке NET = 0 значение выходного сигнала OUT равно нулю (см. рис. 10.4). В отличие от логистической функции гиперболический тангенс принимает значения различных знаков, OUT находится в интервале (-1, 1).