Обучение персептрона
Обучение сети состоит в подстройке весовых коэффициентов каждого нейрона. Пусть имеется набор пар векторов 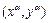 ,
, 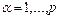 , называемый обучающей выборкой. Будем называть нейронную сеть обученной на данной обучающей выборке, если при подаче на входы сети каждого вектора
, называемый обучающей выборкой. Будем называть нейронную сеть обученной на данной обучающей выборке, если при подаче на входы сети каждого вектора 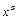 на выходах всякий раз получается соответсвующий вектор
на выходах всякий раз получается соответсвующий вектор 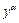 .
.
Предложенный Ф.Розенблаттом метод обучения состоит в итерационной подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах. Алгоритм включает следующие шаги:
| Шаг 0. | Начальные значения весов всех нейронов 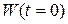 полагаются случайными. полагаются случайными.
|
| Шаг 1. | Сети предъявляется входной 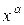 образ, в результате формируется выходной образ образ, в результате формируется выходной образ 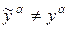 . .
|
| Шаг 2. | Вычисляется вектор ошибки 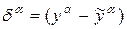 , делаемой сетью на выходе. Идея состоит в том, что изменение вектора весовых коэффициентов в области малых ошибок должно быть пропорционально ошибке на выходе, и равно нулю если ошибка равна нулю. , делаемой сетью на выходе. Идея состоит в том, что изменение вектора весовых коэффициентов в области малых ошибок должно быть пропорционально ошибке на выходе, и равно нулю если ошибка равна нулю.
|
| Шаг 3. | Вектор весов модифицируется по следующей формуле: 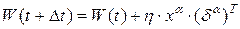 , где , где 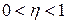 - темп обучения. - темп обучения.
|
| Шаг 4. | Шаги 1 – 3 повторяются для всех обучающих векторов. Один цикл последовательного предъявления всей выборки называется эпохой. Обучение завершается по истечении нескольких эпох, а) когда итерации сойдутся, т.е. вектор весов перестает изменяться, или б) когда суммарная абсолютная ошибка станет меньше некоторого малого значения. |
Используемая на шаге 3 формула учитывает следующие обстоятельства:
а) модифицируются только компоненты матрицы весов, отвечающие ненуле-
вым значениям входов; б) знак приращения веса соответствует знаку ошибки, т.е. положительная ошибка ( 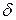 > 0, значение выхода меньше требуемого) приводит к усилению связи; в) обучение каждого нейрона происходит независимо от обучения остальных нейронов.
> 0, значение выхода меньше требуемого) приводит к усилению связи; в) обучение каждого нейрона происходит независимо от обучения остальных нейронов.
Данный метод обучения был назван Ф.Розенблаттом “методом коррекции с обратной передачей сигнала ошибки”. Позднее более широко стало известно название “ 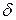 – правило”. Представленный алгоритм относится к широкому классу алгоритмов обучения с учителем, поскольку известны как входные векторы, так и требуемые значения выходных векторов (имеется учитель, способный оценить правильность ответа ученика).
– правило”. Представленный алгоритм относится к широкому классу алгоритмов обучения с учителем, поскольку известны как входные векторы, так и требуемые значения выходных векторов (имеется учитель, способный оценить правильность ответа ученика).
Доказанная Розенблаттом теорема о сходимости обучения по 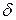 – правилу говорит о том, что персептрон способен обучиться любому обучающему набору, который он способен представить.
– правилу говорит о том, что персептрон способен обучиться любому обучающему набору, который он способен представить.
Дата добавления: 2016-04-22; просмотров: 1039;
