Алгоритм обучения персептрона
Фрэнк Розенблатт предложил алгоритм обучения для одного типа однослойной нейронной сети, получившей название персептрона. Входные значения персептрона являются биполярными (равны -1 или 1), а вес – вещественным числом. Уровень активации персептрона вычисляется как взвешенная сумма его входов, Σxiwi. Выходное значение персептрона вычисляется с помощью строгой пороговой функции: если уровень активации превышает или равен пороговому значению, выход персептрона принимается равным 1, в противном случае – -1. Таким образом, выходное значение персептрона вычисляется на основе его входных значений xi весовых коэффициентов wi, и порога t следующим образом.
1, если Σxiwi ≥ t,
-1, если Σxiwi < t.
Для настройки весов персептрона используется простой алгоритм обучения с учителем. Персептрон пытается решить предлагаемую задачу, после чего ему предъявляется корректный результат. Затем веса персептрона изменяются таким образом, чтобы уменьшить ошибку на его выходе. При этом используется следующее правило.
Пусть
с – постоянный коэффициент скорости обучения,
d – ожидаемое значение выхода.
Настройка весового коэффициента для i-го компонента входного вектора выполняется по формуле
∆wi = c ( d – sign ( Σxiwi )) xi
Здесь sign( Σxiwi ) – выходное значение персептрона, равное +1 или -1. Разность между желаемым и реальным выходными значениями может быть равна 0, 2 или -2. Следовательно, для каждого компонента входного вектора выполняются такие действия.
1. Если значения желаемого и реального выхода совпадают, ничего не происходит.
2. Если реальное выходное значение равно -1, а желаемое 1, то весовой коэффициент для i-го входа увеличивается на 2cxi.
3. Если реальное выходное значение равно 1, а желаемое -1, то весовой коэффициент для i-го входа уменьшается на 2cxi.
При использовании такой процедуры получается вес, минимизирующий среднюю ошибку на всем обучающем множестве. Если существует набор весовых коэффициентов, обеспечивающий корректное выходное значение для каждого элемента обучающего множества, то такая процедура обучения персептрона позволяет его получить.
Первоначально появление персептрона было встречено с большим энтузиазмом. Однако в 1965 году Нильс Нильсон и другие исследователи выявили ограниченность модели персептрона. Они показали, что персептрон не решает целого класса достаточно сложных задач, в которых данные не являются линейно разделимыми. И хотя впоследствии появились различные усовершенствования модели персептрона, в том числе многослойные персептроны, Минский и Пейперт в своей книге "Perceptrons" доказали, что с помощью персептрона нельзя решить проблему линейной разделимости.
Классическим примером задачи классификации, данные которой не обладают свойством линейной разделимости, является проблема "исключающего ИЛИ" (табл. 3). Функцию "исключающего ИЛИ" можно представить с помощью следующей таблицы истинности.
Таблица 3. Таблица истинности для функции "исключающее ИЛИ"
| x1 | x2 | Выход |
Рассмотрим персептрон с двумя входами x1 и x2 , двумя весовыми коэффициентами w1 и w2 и пороговым значением t. Для реализации этой функции сеть должна настроить весовые коэффициенты таким образом, чтобы выполнялись следующие неравенства (рис. 6).
w1*1 + w2*1 < t (из первой строки таблицы истинности),
w1*1 + 0 > t (из второй строки таблицы истинности),
0 + w2*1 > t (из первой строки таблицы истинности),
0 + 0 < t (т.е. положительный порог, из последней строки таблицы истинности).
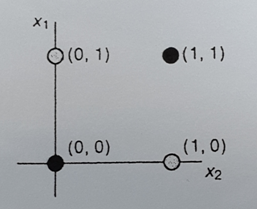
Рис. 6. Задача исключающего ИЛИ
Эта система неравенств для w1 и w2 и t не имеет решения. Тем самым подтверждается, что персептрон не может решить проблему "исключающего ИЛИ". Несмотря на то, что существуют многослойные сети, способные решить эту проблему, алгоритм обучения персептрона предназначен только для обучения однослойных сетей.
Невозможность решения задачи "исключающего ИЛИ" для персептрона объясняется тем, что два класса, которые должна различать сеть, не являются линейно разделимыми (рис. 6). В двухмерном пространстве невозможно провести прямую, разделяющую множества точек с координатами {(0,0), (1,1)} и {(1,0), (0,1)}.
Рис. 10.3. Задача "исключающего ИЛИ". В двухмерном пространстве нельзя провести прямую, разделяющую пары точек {(0,1), (1,0)} и {(0,0), (1,1)}
Дата добавления: 2016-04-14; просмотров: 2623;
