Пример: использование персептронной сети для классификации образов
На рис. 7 показана общая схема решения задачи классификации. Строки данных из пространства возможных точек выбираются и преобразуются к новому виду в пространстве данных и соответствующих им образов. В этом новом пространстве образов выделяются признаки и определяются сущности, представляемые ими. Например, рассмотрим задачу со звуковыми сигналами, записанными на цифровом устройстве. Эти акустические сигналы трансформируются в амплитудно-частотное представление, а затем система классификации по этим признакам может распознать, кому принадлежит данный голос. Еще одним примером задачи классификации является медицинская диагностика, предполагающая сбор информации с помощью медицинского диагностического оборудования и классификацию симптомов по различным категориям болезней.
Для рассматриваемого примера в блоке преобразователя и извлечения признаков на рис. 7 данные из предметной области задачи трансформируются в двухмерные векторы декартова пространства. На рис. 8 показаны результаты анализа информации, приведенной в табл. 4, с помощью персептрона с двумя входами. В первых двух столбцах таблицы содержатся векторы данных, используемые для обучения сети. В третьем столбце представлены ожидаемые результаты классификации, + 1 или -1, используемые для обучения сети. На рис. 8 показаны обучающие данные и линия разделения классов данных, полученных после предъявления обученной сети каждого входного образа.
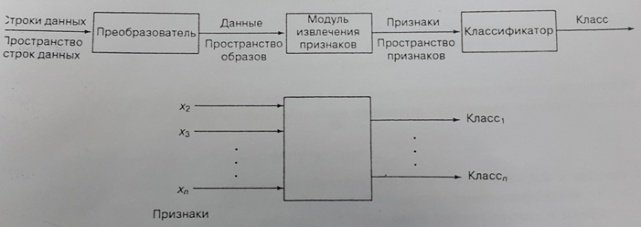
Рис. 7. Полная система классификации
Сначала познакомимся с общей теорией классификации. Каждая группа данных, выявленная классификатором, может быть представлена некоторой областью в многомерном пространстве. Каждому классу Ri соответствует дискриминантная функция gi определяющая степень принадлежности этой области. Среди всех дискриминантных функций для области Ri максимальное значение имеет функция gi :
gi(х) > gj(х) для всех j, 1 < j < n.
В простом примере из табл. 4 двухмерные входные векторы делятся на два класса, первому из которых соответствует значение 1, а второму – -1.
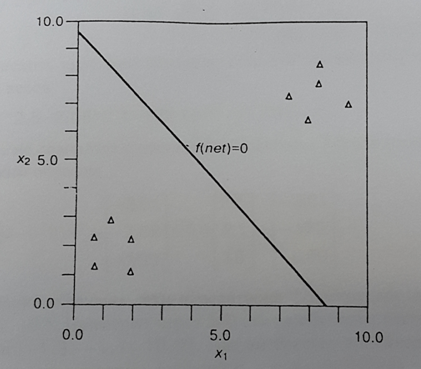
Рис. 8. Данные из табл. 4 в двухмерном пространстве. Персептрон обеспечивает линейное разделение этого набора данных
Таблица 4. Набор обучающих данных для классификации с помощью персептрона
| x1 | x2 | Выход |
| 1,0 | 1,0 | |
| 9,4 | 6,4 | -1 |
| 2,5 | 2,1 | |
| 8,0 | 7,7 | -1 |
| 0,5 | 2,2 | |
| 7,9 | 8,4 | -1 |
| 7,0 | 7,0 | -1 |
| 2,8 | 0,8 | |
| 1,2 | 3,0 | |
| 7,8 | 6,1 | -1 |
Важным частным случаем дискриминантной функции является оценка степени принадлежности на основе расстояния от некоторой центральной точки области. Классификация, основанная на такой дискриминантной функции, называется классификацией по минимальному расстоянию. Легко показать, что такую классификацию можно реализовать для линейно разделимых классов.
Если области Ri и Rj являются смежными, как две области на рис. 8, то существует пограничная область, для которой дискриминантная функция имеет вид
gi(х) = gj(х) или gi(х) - gj(х) = 0.
Если классы линейно разделимы, как на рис. 8, то дискриминантная функция, разделяющая соответствующие области, представляет собой прямую линию, т.е. функции gi и gj являются линейными. Поскольку прямая – это множество точек, равноудаленных от двух фиксированных точек, то дискриминантные функции gi и gj – это функции минимального расстояния от декартового центра каждой из областей.
Линейную разделяющую функцию можно вычислить с помощью персептрона, показанного на рис. 9 и содержащего два обычных входа и пороговый вход с постоянным значением 1. Персептрон выполняет вычисление по следующей формуле
f(net)=f(w1*x1+ w2*x2+ w3*1), где f(x)=sign(x).
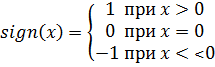
Если f(x)=+1, то х принадлежит одному классу, если f(x)=-1 - другому. Такое преобразование называется кусочно-линейной биполярной пороговой функцией. Пороговый вход служит для смещения пороговой функции вдоль вертикальной оси. Величина этого смещения определяется в процессе обучения с помощью настройки весового коэффициента w3.
Используем данные из табл. 4 для обучения персептрона, показанного на рис. 9. Инициализируем значения веса случайным образом, например [0,75, 0,5, -0,6], и применим алгоритм обучения персептрона, описанный выше. Верхний индекс переменной задает номер текущей итерации алгоритма. Обработка данных начинается с первой строки таблицы
f(net)1=f(0,75*1+ 0,5*1-0,6*1)=f(0,65)=1.
Поскольку значение f(net)1=1 корректно, настройка весовых коэффициентов не нужна. Следовательно, W2=W1. Для второго обучающего примера
f(net)2=f(0,75*9,4+ 0,5*6,4-0,6*1)=f(9,65)=1.
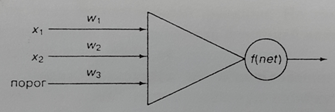
Рис. 9. Персептрон для классификации данных из табл. 10.3 с кусочно-линейной биполярной пороговой функцией
Для данного обучающего примера на выходе персептрона ожидается значение -1, значит, для настройки весов необходимо применить обучающее правило
Wt = Wt-1 + c*( dt-1 – sign ((Wt-1)T*Xt-1)) Xt-1
где с – постоянный коэффициент обучения,
X и W – векторы входов и весовых коэффициентов,
f – номер итерации обучения,
Т – символ транспонирования,
dt-1– ожидаемый результат в момент времени t-1 (или, как в данном случае, в момент времени f=2).
Выход сети при t=2 равен 1, следовательно, разность между ожидаемым и реальным выходом сети составляет d2 – sign ((W2)T*X2).
На самом деле для биполярного персептрона инкремент обучения всегда составляет либо +2сХ либо -2сХ, где X – вектор из обучающего множества. Коэффициент скорости обучения – это небольшое вещественное число, наподобие 0,2. Обновим вектор весовых коэффициентов:
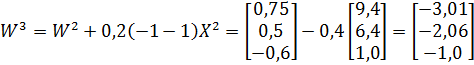
Теперь нужно вычислить выходное значение сети для третьего обучающего примера с учетом настроенных весов
f(net)3=f(-3,01*2,5- 2,06*2,1-1,0*1)=f(-12,84)=-1
Это значение снова не совпадает с ожидаемым выходом. На следующей итерации веса W4 обновляются таким образом
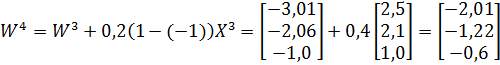
После десяти итераций обучения сети персептрона формируется линейное разделение, показанное на рис. 8. Примерно через 500 шагов обучения вектор весовых коэффициентов будет равен [-1,3; -1,1; 10,9]. Нас интересует линейное разделение двух классов. В терминах дискриминантных функций gi и gj разделяющая поверхность представляет собой множество точек, для которых gi(х)=gj(x) или gi(x)-gj(x)=0, т.е. уровень активации = 0. Уравнение функционирования сети можно записать в терминах весов
net = w1*w1+ w2*w2+ w3
Следовательно, линейная разделяющая поверхность между двумя классами определяется линейным уравнением
-1,3* x1+(-1,1)* x2+10,9=0.
Дата добавления: 2016-04-14; просмотров: 1414;
