Обучение по методу обратного распространения
Среди различных структур нейронных сетей (НС) одной из наиболее известных является многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми аксонами нейронов предыдущего слоя или, в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными. Когда в сети только один слой, алгоритм ее обучения с учителем довольно очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны, и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети. По этому принципу строится, например, алгоритм обучения однослойного перцептрона. В многослойных же сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, не известны, и двух или более слойный перцептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС. Один из вариантов решения этой проблемы – разработка наборов выходных сигналов, соответствующих входным, для каждого слоя НС, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант – динамическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изменяются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный метод "тыка", несмотря на свою кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант – распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения. Именно он будет рассмотрен в дальнейшем.
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:
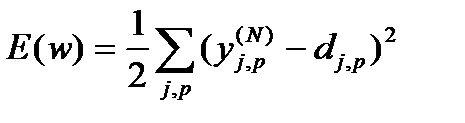 (1)
(1)
где 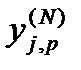 – реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа;
– реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа;
djp – идеальное (желаемое) выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:
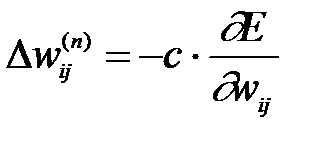 (2)
(2)
Здесь wij – весовой коэффициент синаптической связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n,
с – коэффициент скорости обучения, 0<с<1.
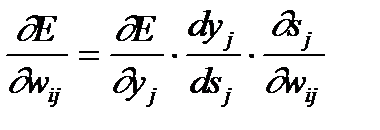 (3)
(3)
yj – выход нейрона j,
sj – взвешенная сумма его входных сигналов, то есть аргумент активационной функции.
Так как множитель dyj/dsj является производной этой функции по ее аргументу, из этого следует, что производная активационной функция должна быть определена на всей оси абсцисс. В связи с этим функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых НС. В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой. В случае гиперболического тангенса
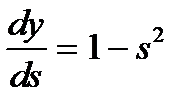 (4)
(4)
Третий множитель ¶sj/¶wij, очевидно, равен выходу нейрона предыдущего слоя yi(n-1).
Что касается первого множителя в (3), он легко раскладывается следующим образом:
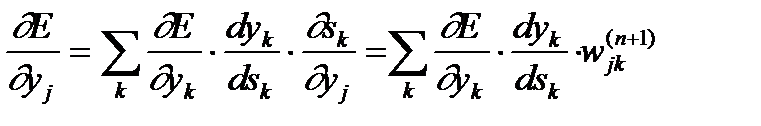 (5)
(5)
Здесь суммирование по k выполняется среди нейронов слоя n+1.
Введя новую переменную
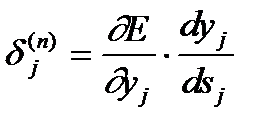 (6)
(6)
получим рекурсивную формулу для расчетов величин dj(n) слоя n из величин dk(n+1) более старшего слоя n+1.
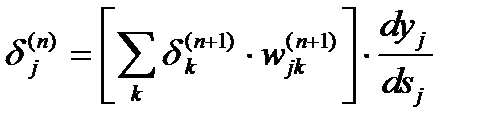 (7)
(7)
Для выходного же слоя
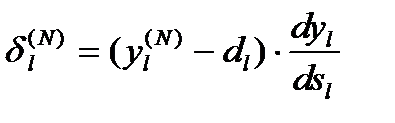 (8)
(8)
Теперь мы можем записать (2) в раскрытом виде:
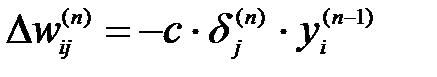 (9)
(9)
Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (9) дополняется значением изменения веса на предыдущей итерации
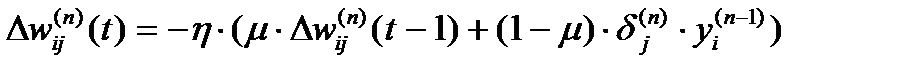 (10)
(10)
где m – коэффициент инерционности,
t – номер текущей итерации.
Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится так:
1. Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Напомним, что
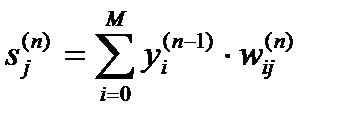 (11)
(11)
где M – число нейронов в слое n-1 с учетом нейрона с постоянным выходным состоянием +1, задающего смещение;
yi(n-1)=xij(n) – i-ый вход нейрона j слоя n.
2. Рассчитать d(N) для выходного слоя по формуле (8).
Рассчитать по формуле (9) или (10) изменения весов Dw(N) слоя N.
 3. Рассчитать по формулам (7) и (9) (или (7) и (10)) соответственно d(n) и Dw(n) для всех остальных слоев, n=N-1,...1.
3. Рассчитать по формулам (7) и (9) (или (7) и (10)) соответственно d(n) и Dw(n) для всех остальных слоев, n=N-1,...1.
4. Скорректировать все веса в НС
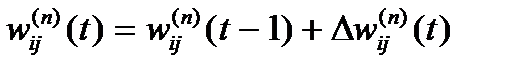 (14)
(14)
5. Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.
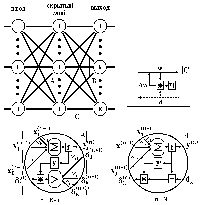
| Рис.10 Диаграмма сигналов в сети при обучении по алгоритму обратного распространения |
Сети на шаге 1 попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других. Алгоритм иллюстрируется рисунком 10.
Применение метода обратного распространения для решения задачи "исключающего ИЛИ"
Рассмотрим задачу "исключающего ИЛИ" и покажем, как ее можно решить с помощью нейронной сети со скрытым слоем. На рис. 11 показана сеть с двумя входными нейронами, одним скрытым и одним выходным элементом. Сеть также содержит два пороговых нейрона, первый из которых связан с единственным нейроном скрытого слоя, а второй – с выходным нейроном. Уровни активации скрытого и выходного нейронов вычисляются обычным образом как скалярное произведение векторов весовых коэффициентов и входных значений. К этому значению добавляется величина порога. Веса обучаются по методу обратного распространения при использовании сигмоидальной активационной функции.
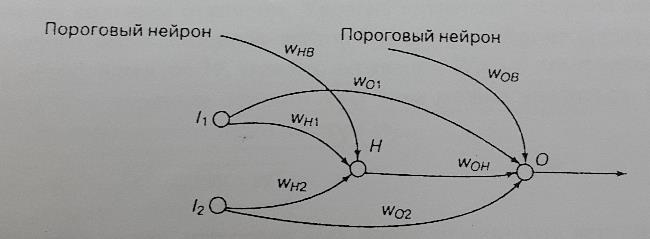
Рис. 11. Решение задачи "исключающего ИЛИ" методом обратного распространения. Здесь Wij - весовые коэффициенты связей, Н - скрытый нейрон
Следует отметить, что входные нейроны напрямую соединены обучаемыми связями с выходным нейроном. Такие дополнительные связи зачастую позволяют снизить размерность скрытого слоя и обеспечивают более быструю сходимость. На самом деле сеть, показанная на рис. 11, не является единственно возможной. Для решения задачи "исключающего ИЛИ" можно подобрать множество различных архитектур нейронных сетей.
Сначала веса связей инициализируются случайным образом, а затем настраиваются с использованием данных из таблицы истинности функции "исключающего ИЛИ"
(0; 0)→0; (1; 0)→1; (0; 1)→1; (1; 1)→0.
После 1400 циклов обучения для этих четырех обучающих примеров получаются весовые коэффициенты следующего вида (значения округлены до 1 знака после запятой)
WH1 = -7,0 ; WHB = 2,6 ; WO1 = -5,0 ; WOH = -11,0 ;
WH2 = -7,0 ; WOB = 7,0 ; WO2 = -4,0.
Для входного вектора (0,0) на выходе скрытого нейрона будет получено значение
f (0*(-7,0)+0*(-7,0)+1*2,6)=f(2,6) →1
Для этого же входного образа выходное значение сети будет вычисляться по формуле
f (0*(-5,0)+0*(-4,0)+1*(-11,0)+1*7,0)=f(-4,0) →0
Для входного вектора (1,0) выходом скрытого нейрона будет
f (1*(-7,0)+0*(-7,0)+1*2,6)=f(-4,4) →0,
а на выходе сети будет получено значение
f (1*(-5,0)+0*(-4,0)+0*(-11,0)+1*7,0)=f(2,0) →1.
Для входного вектора (0; 1) будут получены аналогичные выходные значения. И, наконец, рассмотрим входной вектор (1; 1). Для него на выходе скрытого слоя получим
f (1*(-7,0)+1*(-7,0)+1*2,6)=f(-11,4) →0,
а на выходе сети
f (1*(-5,0)+1*(-4,0)+0*(-11,0)+1*7,0)=f(-2,0) →0.
Понятно, что сеть прямого распространения, обученная по методу обратного распространения ошибки, обеспечивает нелинейное разделение этих данных. Пороговая функция f – это сигмоида, несколько смещенная в положительном направлении за счет обучаемого порога.
Дата добавления: 2016-04-14; просмотров: 1241;
