Нейроны Гроссберга и сети встречного распространения

Для обучения нейронной сети без учителя требуются некоторые начальные знания об области определения задачи. В процессе определения характеристик данных, а также истории обучения идентифицируются классы и выявляются границы между ними. Поскольку данные классифицируются на основе подобия их векторного представления, учитель может поспособствовать в калибровке полученных результатов или в присвоении имен этим классам. Это можно сделать с помощью обучения с учителем, при котором выходы слоя, обучаемого по методу "победитель забирает все", используются в качестве входов второго слоя сети. Решения этого выходного слоя можно явно скоординировать (подкрепить) с помощью учителя.

Такой подход позволяет отобразить результаты слоя Кохонена в выходные образы или классы. Это можно сделать с помощью алгоритма "исходящей звезды" Гроссберга. Комбинированная сеть, включающая слой нейронов Кохонена и слой Гроссберга получила название сети встречного распространения.

На рис. 15 показан слой нейронов А, В, …, N, один из которых – J –является победителем. Алгоритм Гроссберга предполагает наличие обратной связи от учителя, представленной вектором Y, с целью подкрепления весов связей от нейрона J к нейрону I выходного слоя, который должен активизироваться. Согласно алгоритму обучения Гроссберга вес исходящей связи w_ji от нейрона J к нейрону I увеличивается.

В сети встречного распространения сначала обучается слой Кохонена. После определения победителя его выходное значение устанавливается равным 1, а выходные значения всех остальных нейронов Кохонена принимаются равными 0. Нейрон-победитель и все нейроны выходного слоя, с которыми он связан, формируют так называемую "исходящую звезду" (рис. 15). Обучение слоя Гроссберга осуществляется для компонентов этой "звезды".

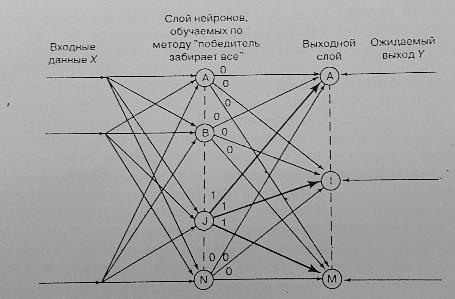
Рис. 15. "Исходящая звезда" для нейрона J в сети, обучаемой по методу "победитель забирает все". Вектор Y- это ожидаемый выход слоя Гроссберга. Жирной линией выделены связи нейрона, выход которого равен 1; выходные значения всех остальных нейронов слоя Кохонена равны 0

Если каждый кластер входных векторов представляется одним классом и всем членам этого класса соответствует одно и то же значение выходного слоя, то в итеративном обучении нет необходимости. Требуется лишь определить, с каким нейроном слоя Кохонена связан каждый класс, а затем назначить веса связей между каждым нейроном-победителем и выходным слоем на основе ассоциации между классами и ожидаемыми выходными значениями. Например, если J-й нейрон Кохонена соответствует всем элементам кластера, для которого ожидаемым выходом сети является I=1, то для связи между нейронами J и I нужно установить значение w_ji= 1, а для всех остальных весовых коэффициентов исходящих связей нейрона

J–w_jk= 0.

Если одному кластеру могут соответствовать различные выходные нейроны, то для настройки весовых коэффициентов "исходящей звезды" применяется итеративная процедура обучения с учителем на основе ожидаемого вектора Y. Целью процедуры обучения является усреднение ожидаемых выходных значений для элементов каждого кластера. Веса связей нейрона-победителя с выходными нейронами настраиваются согласно формуле

W^t+1=W^t+c(Y-W^t),

где с – малый положительный коэффициент обучения,

W^t – вектор весовых коэффициентов связей нейрона-победителя с выходным слоем,

Y – ожидаемый выходной вектор.

Заметим, что этот алгоритм обучения приводит к усилению связей между узлом J слоя Кохонена и узлом I выходного слоя только в том случае, если I – нейрон-победитель, и его выход равен 1, а желаемый выход при этом тоже равен 1.

Сеть встречного распространения имеет, в некотором смысле, значительное преимущество перед сетью обратного распространения. Подобно сети обратного распространения, она обучается классификации на основе нелинейного разделения. Однако делается это за счет препроцессинга, обеспечиваемого слоем Кохонена, с помощью которого данные делятся на кластеры. Такая кластеризация обеспечивает существенное преимущество по сравнению с сетью обратного распространения, поскольку устраняет необходимость выполнения поиска, требуемого для обучения скрытых слоев такой сети.