Двунаправленная ассоциативная память
Двунаправленная ассоциативная память (ДАП) состоит из двух полносвязных слоев обрабатывающих элементов. Может также существовать обратная связь каждого нейрона с самим собой. Сеть ДАП, отображающая n-мерный входной вектор Хn в m-мерный выходной вектор Ym, показана на рис.20. Поскольку связи между нейронами слоев X и Y являются двунаправленными, то веса связей необходимо определять для обоих направлений.
Рис. 20. Сеть ДАП для примера из подраздела 10.6.2. Каждый нейрон может быть связан с самим собой
Подобно весам в линейном ассоциаторе, веса связей в сети ДАП можно вычислить заранее. Для определения весов используется тот же метод, что и в линейной ассоциативной модели. Векторы состояний в архитектуре ДАП рассматриваются в хемминговом пространстве.
Пусть даны N пар векторов, составляющих набор эталонов, которые необходимо сохранить в памяти. Веса связей вычислим следующим образом:
W=Y1*X1+ Y2*Х2+...+ Yt*Хt
Это соотношение позволяет вычислить веса связей от слоя X к слою Y (см. рис. 20). Например, W32 – это вес связи, ведущий от третьего нейрона слоя X ко второму нейрону слоя Y. Предполагается, что между двумя нейронами существует лишь одна связь. Следовательно, весовые коэффициенты связи между слоями X и Y одинаковы в обоих направлениях, т.е. матрица весов связей, ведущих от слоя Y к слою X, является транспонированной матрицей W.
Сеть ДАП используется для извлечения из памяти образов при подаче входного образа на вход слоя X. Если входной образ зашумлен или неполон, то сеть ДАП зачастую может восполнить этот образ и извлечь из памяти связанный с ним вектор.
Чтобы извлечь данные из памяти сети ДАП, нужно выполнить следующие действия.
1. В нейронную сеть передается исходная пара векторов (X,Y), где X – это образ, для которого нужно восстановить связанный с ним эталон, а Y – случайно заданный вектор.
2. Информация распространяется от слоя X к слою Y, и вычисляются значения нейронов слоя Y.
3. Выходные значения нейронов слоя Y передаются на вход слоя X, и вычисляются значения нейронов этого слоя.
4. Два предыдущих действия продолжают выполняться до тех пор, пока состояние сети не стабилизируется, т.е. значения векторов X и Y перестанут изменяться.
Указанный алгоритм описывает распространение информации в сети ДАП в обоих направлениях до достижения точки равновесия. Работу алгоритма можно начинать с передачи в сеть значений слоя Y, тогда после сходимости можно получить значение вектора X. Эта сеть в полном смысле является двунаправленной: в качестве входа можно использовать вектор X и вычислять ассоциированный с ним вектор Y, а можно на основании вектора Y определять значение вектора X.
После сходимости процесса обработки состояние равновесия представляет собой один из эталонов, использованных для построения исходной матрицы весов. На вход сети подается вектор с известными свойствами: либо идентичный одному из векторов эталонной пары, либо слегка отличный от него. Этот вектор используется для восстановления второго вектора из эталонной пары. В качестве расстояния выбирается хеммингово расстояние, измеряемое как количество различающихся элементов векторов. Благодаря свойству ортонормированности сходимость сети ДАП к одному вектору означает также сходимость к его дополнению. Следовательно, вектор дополнения тоже становится аттрактором сети.
Сходимость сети ДАП определяется несколькими факторами. Если в матрице весов сохранено слишком много эталонов, то они оказываются очень близки друг к другу, что приводит к появлению псевдоустойчивых состояний в сети. Этот феномен получил название помех, которые приводят к появлению локальных минимумов в пространстве энергии сети.
Обработка информации в сети ДАП происходит следующим образом. Умножая входной вектор на матрицу связей, получим входные значения элементов второго слоя. Простая пороговая функция приводит полученный результат к виду, необходимому для хранения вектора в хемминговом пространстве.
net(Y)=WY,или для каждого элемента yi net(yi)=∑wij*xj
Аналогичное соотношение справедливо для вычисления значения нейронов слоя X. Пороговая функция в момент времени t+1 имеет вид
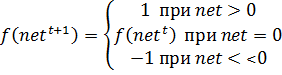
Дата добавления: 2016-04-14; просмотров: 1130;
