Пример алгоритма обучения Хебба без учителя

При обучении без учителя для корректировки выходных значений не используется внешнее воздействие. Веса модифицируются исключительно на основе информации о входах и выходах нейрона. Обучение такой сети сводится к усилению отклика сети на уже "виденные" образы. В следующем примере будет показано, как метод Хебба используется для моделирования обучения на основе обусловленного отклика, когда в роли условия для желаемого отклика выступает произвольно выбранный стимул.

При обучении Хебба без учителя веса нейрона i можно настраивать по формуле

∆W = c*f ( X, W)*X,

где с – малый положительный коэффициент обучения,

f(X, W) – выходное значение i-го нейрона,

X – вход i-го нейрона.

Обучение Хебба можно использовать для преобразования отклика сети из вида основного или безусловного стимула к условному. Это позволит промоделировать метод обучения, разработанный при экспериментах Павлова, когда у собаки вырабатывался условный рефлекс на звонок. После того, как подача пищи собаке многократно сопровождалась звонком, при звуке звонка у нее начиналось слюноотделение. Сеть, показанная на рис. 10.18, содержит два слоя: входной слой с шестью нейронами и выходной слой с одним нейроном. Выходной нейрон может принимать значение +1, соответствующее возбужденному состоянию этого нейрона, и -1, соответствующее его невозбужденному состоянию.

Примем коэффициент скорости обучения равным 0,2. В этом примере сеть обучается на образ [1;-1;1;-1;1;-1], представляющий собой конкатенацию двух образов: [1;-1;1] и [-1;1;-1]. Образ [1;-1;1] соответствует безусловному стимулу, а образ [-1;1;-1] – новому.

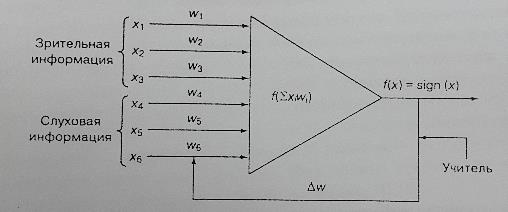
Рис. 16. Пример нейронной сети, для которой применяется обучение Хебба без учителя

Предположим, сеть положительно реагирует на безусловный стимул, но не воспринимает новый стимул. Положительный отклик сети на безусловный стимул можно обеспечить с помощью весового вектора [1;-1;1], в точности соответствующего входному образу, а нейтральный отклик на новый стимул – с помощью вектора весов [0;0;0]. Конкатенация этих двух векторов весовых коэффициентов дает исходный вектор весов сети

[1;-1;1;0;0;0].

Теперь сеть нужно обучить реакции на входной образ таким образом, чтобы новая конфигурация весов обеспечивала положительный отклик на новый стимул. На первом шаге работы сети вычислим

W*Х=(1*1)+((-1)*(-1))+(1*1)+(0*(-1))+(0*1)+(0*(-1))= (1)+(1)+(1)=3,

f(3)=sign(3)=1.

Теперь определим новый вектор весовых коэффициентов W²

W²=[1;-1;1;0;0;0]+0,2*1*[1;-1;1;-1;1;-1]=

=[1;-1;1;0;0;0]+[0,2;-0,2;0,2;-0,2;0,2;-0,2]=[1,2;-1,2;1,2;-0,2;0,2;-0,2].

Вычислим отклик сети на тот же входной образ с учетом обновленного вектора весов

W*Х=(1,2*1)+((-1,2)*(-1))+(1,2*1)+((-0,2)*(-1))+(0,2*1)+((-0,2)*(-1))=

=(1,2)+(1,2)+(1,2)+(0,2)+(0,2)+(0,2)=4,2,

f(4,2)=1.

Определим новый вектор весовых коэффициентов W³

W³=[1,2;-1,2;1,2;-0,2;0,2;-0,2]+0,2*1*[1;-1;1;-1;1;-1]=

=[1,2;-1,2;1,2;-0,2;0,2;-0,2]+[0,2;-0,2;0,2;-0,2;0,2;-0,2]=

=[1,4;-1,4;1,4;-0,4;0,4;-0,4].

Несложно заметить, что произведение векторов W*X продолжает возрастать, при этом абсолютное значение каждого элемента вектора весовых коэффициентов в каждом цикле обучения увеличивается на 0,2. После 13 итераций обучения вектор весовых коэффициентов примет вид

W¹³=[3,4;-3,4;3,4;-2,4;2,4;-2,4].

Теперь этот обученный вектор весов можно использовать для тестирования отклика сети на два отдельных образа. При этом ожидается, что сеть будет по-прежнему положительно реагировать на безусловный стимул, и, что гораздо важнее, будет давать положительный отклик на новый, обусловленный, стимул. Сначала проверим реакцию сети на безусловный стимул [1;-1;1]. Три последних элемента входного вектора заполним произвольно выбранными значениями 1 и -1. Например, определим реакцию сети на вектор [1;-1;1;1;1;-1]

sign(W*X)=sign((3,4*1)+((-3,4)*(-1))+(3,4*1)+(-2,4*1)+(2,4*1)+((-2,4)*(-1)))= =sign(3,4+3,4+3,4-2,4+2,4+2,4)= sign(12,6)= +1.

Таким образом, сеть по-прежнему положительно реагирует на исходный безусловный стимул. Теперь проверим реакцию сети на тот же безусловный стимул и другой случайно выбранный вектор в последних трех позициях [1;-1;1;1;-1;-1]

sign(W*X)=sign((3,4*1)+((-3,4)*(-1))+(3,4*1)+(-2,4*1)+(2,4*(-1))+((-2,4)*(-1)))= =sign(3,4+3,4+3,4-2,4-2,4+2,4)= =sign(7,8)=+1.

Этот входной вектор тоже приводит к положительному отклику сети. На самом деле эти два примера свидетельствуют о том, что сеть чувствительна к исходному стимулу, связь с которым была усилена благодаря его многократному повторению.

Теперь определим отклик сети на новый стимул [-1;1;-1], закодированный в последних трех позициях входного вектора. Первые три элемента заполним случайно выбранными значениями из множества {-1;1} и проверим реакцию сети на входной вектор [1;1;1;-1;1;-1]

sign(W*X)=sign((3,4*1)+((-3,4)*1)+(3,4*1)+(-2,4*(-1))+(2,4*1)+((-2,4)*(-1)))= =sign(3,4-3,4+3,4+2,4+2,4+2,4)= sign(10,6)= +1.

Второй стимул тоже успешно распознан!

Проведем еще один эксперимент, слегка изменив входной вектор. Этот случай будет соответствовать ситуации, когда используется новый вид еды и другой тип звонка. Протестируем сеть на входном векторе [1;-1;-1;1;1;-1], где первые три элемента не совпадают с исходным стимулом, а вторые три отличаются от обусловленного

sign(W*X)=sign((3,4*1)+((-3,4)*(-1))+(3,4*(-1))+(-2,4*1)+(2,4*1)+((-2,4)*(-1)))= =sign(3,4+3,4-3,4-2,4+2,4+2,4)=sign(5,8)=+1.

Следовательно, распознан даже слегка отличный стимул.

Благодаря многократному совместному появлению старого и нового стимула была создана ассоциация между новым стимулом и старым откликом. Сеть научилась обеспечивать прежний отклик на новый стимул без участия учителя. Такая повышенная чувствительность также позволяет сети правильно отвечать на слегка модифицированный стимул. Это достигается за счет синхронного обучения Хебба, в процессе которого сила отклика на общий образ увеличивается, что приводит к усилению отклика сети на каждый отдельный компонент этого образа.