Ассоциативная память и линейный ассоциатор

Нейронная сеть, представляющая собой линейный ассоциатор, впервые была предложена Т. Кохоненом и Дж. Андерсоном.

Введем несколько определений, связанных с хранением информации в памяти. Входные образы и хранимые в памяти значения являются векторами. Для устранения проблемы представления обычно вводится индуктивный порог, предполагающий задание множества векторов признаков. Хранимые в памяти ассоциации представляются в виде набора векторных пар {<Х₁, Y₁>, <Х₂, Y₂>, …, <Х_t , Y_t>}. Для каждой пары векторов <Х_i,Y_i> образ X_i – это ключ для восстановления образа Y_i. Существует три типа ассоциативной памяти.

1. Гетероассоциативная память – это такое отображение, при котором вектору X, наиболее близкому к Х_i ставится в соответствие возвращаемый вектор Y_i.

2. Автоассоциативная память – это такое отображение, при котором для всех пар Х_i = Y_i. Поскольку каждый вектор Х_i ассоциируется с самим собой, эта форма памяти используется в основном для восстановления полного вектора по его части.

3. Интерполятивная память – это такое отображение Ф: Х→Y, при котором отличному от эталона вектору Х=Х_i+Δi, ставится в соответствие выходной вектор Ф(Х) = Ф(Х_i+Δi) = Y_i+E, где Е=Ф(Δi). При интерполятивном отображении каждый из ключей эталона связывается с соответствующим образом в памяти. Если же входной вектор отличается от эталонного на вектор Δ, то выходyой вектор тоже отличается от эталонного на величину Е, где Е=Ф(Δ_i).

Автоассоциативная и гетероассоциативная память используются для восстановления одного из запомненных эталонов. Они моделируют память в ее исходном значении, при котором извлекаемый образ является точной копией запомненного. Можно также сконструировать память таким образом, чтобы выходной вектор отличался от сохраненного в памяти в некотором семантическом смысле. В этом и состоит роль интерполятивной памяти.

Линейный ассоциатор, представленный на рис. 18, реализует одну из форм интерполятивной памяти. Его работа основана на модели обучения Хебба. Веса связей инициализируются с помощью соотношения

W=Y₁*X₁+ Y₂*Х₂+...+ Y_t*Х_t.

При таких значениях весовых коэффициентов для каждого эталонного ключа сеть будет восстанавливать точно соответствующий ему эталонный образ, в противном случае она будет осуществлять интерполяционное отображение.

Теперь введем несколько понятий, которые помогут проанализировать поведение этой сети. Сначала введем метрику, позволяющую определить точное расстояние между векторами. Все векторы-эталоны в рассмотренном примере являются хемминговыми, т.е. состоящими только из -1 и +1. Для описания расстояния между хемминговыми векторами можно ввести хеммингово расстояние. Определим хеммингово пространство следующим образом:

Н_n={Х=(х₁,х₂,...,х_n)},

где каждый элемент х_i принимает значения из множества {+1;-1}.

Хеммингово расстояние определяется между двумя любыми векторами в хемминговом пространстве как

||Х, Y|| = количеству различных компонентов в векторах X и Y.

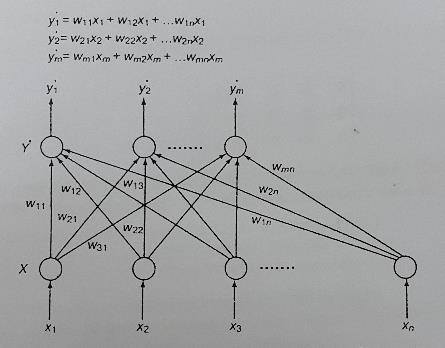
Рис. 18. Линейная ассоциативная сеть. На вход сети подается вектор Xi, а на выходе получается соответствующий ему вектор Yi каждый компонент которого yi является линейной комбинацией входов. В процессе обучения каждый выходной нейрон подкрепляется соответствующими ему корректными выходными сигналами

Например, хеммингово расстояние в четырехмерном хемминговом пространстве между векторами

(1;-1;-1;1)и{1;1;-1;1) равно 1,

(-1;-1;-1;1) и (1;1;1-;1) равно 4,

(1;-1;1;-1) и (1;-1;1;-1) равно 0.

Дополнением хеммингового вектора называется вектор, все компоненты которого противоположны компонентам исходного вектора. Например, дополнением к (1;-1;-1;-1) является вектор (-1;1; 1;1).

Ортонормальными называются ортогональные или перпендикулярные векторы единичной длины. Покомпонентное произведение ортонормальных векторов равно 0. Следовательно, скалярное произведение любых двух векторов X_i и Х_j из набора ортонормальных векторов равно 0, если эти векторы различны:

X_iX_j=δ_ij,

где δ_ij=1, если i=j, и δ_ij=0 в остальных случаях.

Покажем, что определенный выше линейный ассоциатор обладает следующими двумя свойствами. Пусть Ф(Х)– выполняемое сетью отображение. Во-первых, для любого входного вектора Х_i, точно соответствующего одному из эталонов, выход сети Ф(Х_i) равен соответствующему выходному эталонному вектору Y_i. Во-вторых, для любого входного вектора X_k, не соответствующего ни одному из эталонов, выход сети Ф(Хk) равен вектору Y_k, представляющему собой интерполяцию вектора X_k. Более точно, для X_k = Х_i+Δi, где Х_i – эталонный вектор, сеть возвращает значение

Y_k=Y_i+E, где Е=Ф(Δ_i).

Сначала покажем, что при подаче на вход сети одного из эталонов она возвращает соответствующий ему эталонный образ.

По определению активационной функции сети

Ф(Х_i)=WX_i

Поскольку

W=Y₁*X₁+ Y₂*Х₂+...+ Y_n*Х_n,

получим

Ф(Х_i)=(Y₁*X₁+ Y₂*Х₂+...+ Y_n*Х_n) X_i= Y₁*X₁*X_i + Y₂*Х₂*X_i +...+ Y_n*Х_n*X_i

по закону дистрибутивности. Поскольку из сказанного выше следует, что X_iX_j=δ_ij, то

Ф(Х_i)= Y₁*δ_1i + Y₂*δ_2i +...+ Y_n*δ_ni

По условию ортонормальности δ_ij=1 при i=j и 0 в остальных случаях. Тогда

Ф(Х_i)= Y₁*0 + Y₂*0 +…+ Y_i*1+….+Y_n*0= Y_i

Можно также показать, что для входного вектора X_k, не соответствующего ни одному из эталонов, сеть выполняет интерполирующее отображение. Так, для X_k = Х_i+Δi , где Х_i – один из эталонных векторов

Ф(Х) = Ф(Х_i+Δi) = Y_i+E

где Y_i – вектор, связанный с X_i, а

E= Ф(Δ_i)=(Y₁*X₁+ Y₂*Х₂+...+ Y_n*Х_n) Δ_i

Теперь приведем пример обработки данных с помощью линейного ассоциатора. На рис. 19 показана простая линейная ассоциативная сеть, отображающая четырехмерный вектор X в трехмерный вектор Y. Поскольку сеть работает в хемминговом пространстве, в качестве активационной функции необходимо использовать описанную выше функцию sign.

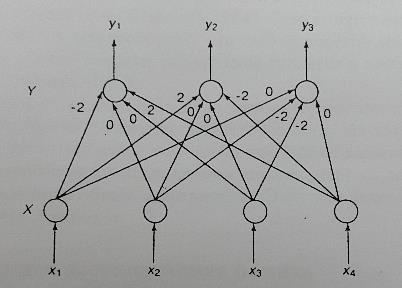
Рис. 19. Линейный ассоциатор

Допустим, требуется запомнить две векторные ассоциации <Х₁, Y₁>, <Х₂, Y₂>, где

X₁=[1;-1;-1;-1]↔Y₁=[-1;1;1],

X₂=[-1;-1;-1;1]↔Y₂=[1;-1;1].

Используя определенную в предыдущем разделе формулу инициализации весов для линейного ассоциатора, получим

W=Y₁*X₁+ Y₂*Х₂+...+ Y_n*Х_n

С помощью операции внешнего векторного произведения Y₁X₁+Y₂X₂ вычислим весовую матрицу сети

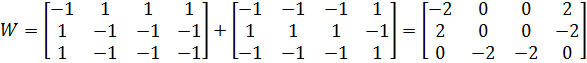
Проверим работу линейного ассоциатора для одного из эталонов. Начнем с вектора Х=[1;-1;-1;-1] из первой эталонной пары и вычислим связанный с ним вектор Y.

y₁=((-2)*1)+(0*(-1))+(0*(-1))+(2*(-1))=-4, sign(-4)=-1,

у₂=(2*1)+(0*(-1))+(0*(-1))+((-2)*(-1))=4, sign(4)=1,

у₃=(0*1)+((-2)*(-1))+((-2)*(-1))+(0*(-1))=4, sign(4)=1.

Следовательно, Y₁=[-1;1;1] – получена вторая половина пары.

Приведем пример линейной интерполяции эталона. Рассмотрим вектор Х=[1;-1;1;1].

y₁=((-2)*1)+(0*(-1))+(0*1)+(2*1)=0, sign(0)=1.

у₂=(2*1)+(0*(-1))+(0*(-1))+((-2)*1)=0, sign(0)=1,

у₃=(0*1)+((-2)*(-1))+((-2)*1)+(0*1)=0, sign(0)=1.

Заметим, что вектор Y=[1;1;1] не соответствует ни одному из эталонов.

Ожидаемые свойства таких сетей основываются на предположении, что эталонные экземпляры составляют множество ортонормальных векторов. Это ограничивает их практическую применимость по двум причинам. Во-первых, может не существовать очевидного отображения реальной жизненной ситуации в ортонормированный набор векторов. Во-вторых, количество сохраняемых образов ограничено размерностью векторного пространства. Если требование ортонормированности нарушается, образы смешиваются в памяти, что приводит к помехам (crosstalk).

Линейный ассоциатор восстанавливает эталонный образ только тогда, когда входной вектор в точности соответствует эталонному. При отсутствии точного соответствия входного вектора сеть выполняет интерполяционное отображение. Можно возразить, что интерполяция не является памятью в прямом смысле этого слова. Зачастую требуется реализовать истинные свойства памяти, когда при подаче на вход приближенного ключа сеть восстанавливает точный соответствующий ему эталонный образ. Для этого нужно ввести в рассмотрение аттракторный радиус, обеспечивающий притяжение векторов из некоторой окрестности.

Аттракторные сети (сети "ассоциативной памяти")

До сих пор рассматривались сети прямого распространения информации. В таких сетях данные поступают на входные нейроны, и сигнал распространяется к последующим слоям до выхода из сети. Еще одним важным классом нейронных сетей являются сети с обратными связями. Архитектура таких сетей отличается тем, что выходной сигнал передается прямо или косвенно назад, ко входам нейрона.

Отличия сетей с обратными связями от сетей прямого распространения состоят в следующем.

1. Между нейронами существуют обратные связи.

2. Имеется некоторая временная задержка, т.е. сигнал распространяется не мгновенно.

3. Выходом сети является ее состояние по завершении процесса сходимости.

4. Полезность сети зависит от свойств сходимости.

Когда сеть с обратными связями приходит к неизменному состоянию, такое состояние называется состоянием равновесия, которое и рассматривается в качестве выхода сети.

В сетях с обратными связями состояния сети инициализируются входным вектором. Сеть обрабатывает этот образ, передавая его несколько раз от входа к выходу до тех пор, пока не достигнет состояния равновесия. Состояние равновесия сети – это и есть образ, извлеченный из памяти.

Аттрактор – это состояние, к которому со временем сходятся другие состояния из некоторой окрестности. Каждому аттрактору в сети соответствует область, внутри которой сеть всегда эволюционирует к этому состоянию. Эта область характеризуется аттракторным радиусом. Аттрактор может содержать одно состояние сети или несколько состояний, по которым происходит циклическое перемещение.