Автомат с магазинной памятью

КС-языки можно распознавать с помощью автомата с магазинной памятью (МП-автомата).

3.3.1 Определение МП-автомата

Определение МП-автомат можно представить в виде семерки:

,

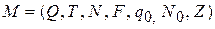где Q – конечное множество состояний автомата;

T – конечный входной алфавит;

N – конечный магазинный алфавит;

F – магазинная функция, отображающая множество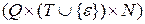

во множество всех подмножеств множества 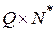, т.е.

® ;

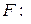
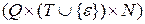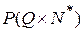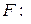q₀ – начальное состояние автомата, q₀ ÎQ;

N₀– начальный символ магазина, N₀ Î N;

Z – множество заключительных состояний автомата, Z Í Q.

Определение Конфигурацией МП-автомата называется тройка вида:

,

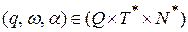где q – текущее состояние автомата, q Î Q;

w - часть входной строки, первый символ которой находится под входной головкой,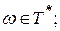

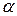- содержимое магазина,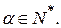

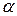Общая схема МП-автомата представлена на рисунке 3.1.

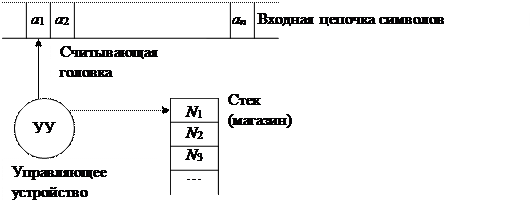Рисунок 3.1 – Схема МП-автомата

Алгоритм Функционирование МП-автомата

Начальной конфигурацией МП-автомата является конфигурация (q₀, 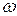, N₀).

Шаг работы МП-автомата будем представлять в виде отношения непосредственного следования конфигураций (обозначается «|=») и отношения достижимости конфигураций (обозначается «|=*»). Если одним из значений магазинной функции 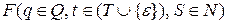является 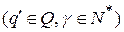, то записывается 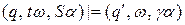. При этом возможны следующие варианты.

1) Случай t Î T. Автомат находится в текущем состоянии q, читает входной символ t, имеет в вершине стека символ S. Он переходит в очередное состояние 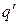, сдвигает входную головку на ячейку вправо и заменяет верхний символ S строкой 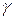магазинных символов. Вариант 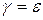означает, что S удаляется из стека.

2) Случай 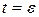. Отличается от первого случая тем, что входной символ t просто не принимается во внимание, и входная головка не сдвигается. Такой шаг работы МП-автомата называется -шагом, который может выполняться даже после завершения чтения входной строки.

Заключительной конфигурацией МП-автомата является конфигурация (q, , 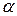), где q Î Z.

Определение МП-автомат допускает входную стоку 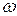, если существует путь по конфигурациям 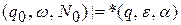для некоторых q Î Z и .

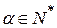Определение Язык L, распознаваемый (принимаемый) МП-автоматом М определяется как множество вида:

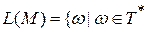и 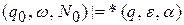для некоторых q Î Z и }.

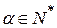3.3.2 Разновидности МП-автоматов

Иногда определяют МП-автомат, который принимает строку, если после завершения ее чтения стек автомата будет пуст. В этом случае нет необходимости выделять множество заключительных состояний Z 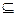Q, а описание заключительной конфигурации имеет вид (q, 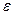, 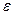), где q 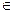Q. Говорят, что такой МП-автомат принима­ет строку языка опустошением магазина.

ПримерМП-автомат 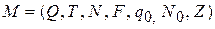,где

Q= {А} Т= {(,)}, N= {I,0}, q_o = A, N₀ = I,

F={ F(A,(,I)=(A,OI)

F(A,(,O)=(A,OO)

F(A,),O)=(A, )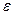

F(A, 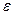,I)=(A, )}

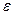при распознавании строки (()()) строит последовательность конфигураций: (А, (() ()), I) |- (А, () () ), 01) |- (А,) ()), OOI) |- (А, ()), OI) |- (A,)), OOI) |- (А, ),О1) |- (А, 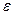, I) |- (А, , ).

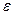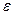Язык, принимаемый МП-автоматом в данном примере, это КС-язык парных круглых скобок. Этот же язык генерирует КС-грамматика с правилами Р = {S ->(S), S-> SS, S -> }.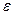

Из формального определения МП-автомата следует, что он может менять каждый раз только один символ в вершине стека. Этот МП-автомат не может, кроме того, продолжать работу при пустом стеке, так как 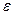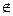N. Однако если использовать расширенный МП-автомат, т.е. МП-автомат с магазинной функцией 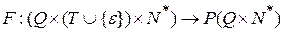,то указанные ограничения будут сняты.

Определение МП-автомат с магазинной функцией 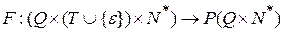называется расширенным МП-автоматом, т.е. автоматом, который может заменять цепочку символов конечной длины в верхушке стека на другую цепочку символов конечной длины.

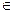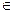МП-автомат называют детерминированным (ДМП-автоматом), если, находясь в любой конфигурации, он может выбрать не более одной следующей конфигурации. Это означает, что при любых значениях q Q, а (T 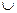{ 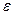}) и 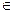N₀ N |N₀ 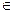N* (для расши­ренного автомата) магазинная функция 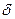(q, a, Z) имеет не более одного значения. В противном случае МП-автомат является не­детерминированным.

Доказано соответствие КС-грамматик и МП-автоматов, которое можно сформулировать так: существуют КС-языки, МП-автоматы и расширенные МП-автоматы, определяющие один и тот же КС-язык.

3.3.3 Взаимосвязь МП-автоматов и КС-грамматик

3.3.3.1 Построение МП-автомата по КС-грамматике

Построим МП-автомат, выполняющий левосторонний разбор. Данный автомат обладает только одним состоянием и принимает входную строку опустошением магазина. Стек используется для размещения текущей сентенции, первоначально это начальный символ грамматики. Очередная сентенция получается заменой верхнего нетерминала стека.

Вход: КС-грамматика .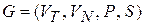

Выход: МП-автомат 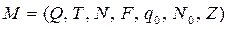такой, что L(M) = L(G).

Шаг 1. Положить Q = {q}, q₀ = q, Z = Æ, N = V_T È V_N, T = V_T, N₀ = S.

Шаг 2. Для каждого правила вида (А® 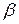) 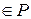, где сформировать магазинную функцию вида 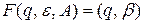. Эти функции предписывают замещать нетерминал в вершине стека по правилу грамматики.

Шаг 3. Для каждого t 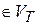сформировать магазинную функцию вида 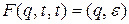, которая выталкивает из стека символ, совпадающий с входным, и перемещает читающую головку. Эти функции обеспечивают опустошение стека.

Пример Дана КС-грамматика:

G({+, (, ), a}, {S, A}, {S®S+A | A, A®(S) | a},{S}). Последовательность построения МП-автомата будет иметь вид.

1) Q = {q}, q₀ = q, T = {+, (, ), a }, N = {+, (, ), a, S, A}, N₀ = S, Z = Æ.

2) F(q, , S) = (q, S+A), F(q, , S) = (q, A), F(q, , A) = (q,(S)); F(q, , A) = (q, a).

3) F(q, t, t) = (q, ) для каждого t Î{+, (, ), a}.

Распознавание строки (а) построенным МП-автоматом представлено в таблице 3.1. Полученный МП-автомат является недетерминированным.

Таблица 3.1 – Распознавание МП-автоматом строки (а)

Номер конфигурации	Текущее состояние	Входная строка	Содержимое магазина
	q	(a)	S
	q	(a)	A
	q	(a)	(S)
	q	a)	S)
	q	a)	A)
	q	a)	a)
	q	)	)
	q

3.3.3.2 Построение расширенного МП-автомата по КС-грамматике

Построим МП-автомат, выполняющий правосторонний разбор. Данный автомат имеет единственное текущее состояние и одно заключительное состояние, в котором стек пуст. Стек содержит левую часть текущей сентенции. Первоначально в стек помещается специальный магазинный символ, маркер пустого стека #. На каждом шаге автомат по правилу грамматики замещает нетерминалом строку верхних символов стека или дописывает в вершину входной символ.

Вход: КС-грамматика .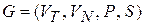

Выход: расширенный МП-автомат 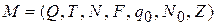такой, что L(M) = L(G).

Шаг 1. Положить Q = {q, r}, q₀ = q, Z = {r}, N = V_T È V_N È {#}, T = V_T, N₀ = #.

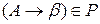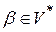Шаг 2. Для каждого правила вида , где , сформировать магазинную функцию вида 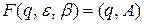, предписывающую заменять правую часть правила в вершине стека нетерминалом из левой части, независимо от текущего символа входной строки.

Шаг 3. Для каждого терминала 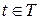сформировать магазинную функцию вида 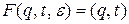, которая помещает символ входной строки в вершину стека, если там нет правой части правила, и перемещает читающую головку.

Шаг 4. Предусмотреть магазинную функцию для перевода автомата в заключительное состояние .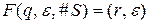

Пример Для грамматики из предыдущего примера построить расширенный МП-автомат. Последовательность построения МП-автомата будет иметь вид.

1) Q = {q, r}, q₀ = q, T = {+, (, ), a}, N = {+, (, ), a, S, A}, N₀ = #, Z = r.

2) F(q, , S+A) = (q, S), F(q, , A) = (q, S), F(q, , (S)) = (q, A), F(q, , a) =(q, A).

3) F(q, t, ) = (q, t) для каждого t Î{+, (, ), a}.

4) F(q, , #S) = (r, ).

Распознавание строки (а) расширенным МП-автоматом представлено в таблице 3.2. Полученный МП-автомат является детерминированным.

Таблица 3.2 – Распознавание расширенным МП-автоматом строки (а)

Номер конфигурации	Текущее состояние	Входная строка	Содержимое магазина
	q	(a)	#
	q	a)	#(
	q	)	#(a
	q	)	#(A
	q	)	#(S
	q		#(S)
	q		#A
	q		#S
	r