Обучение Хебба с учителем

Правило обучения Хебба основано на принципе усиления связи между нейронами при их взаимном возбуждении. Этот принцип можно адаптировать и к обучению с учителем, если вес связи настраивать на ожидаемый, а не реальный выход нейрона. Например, если входной потенциал нейрона В, поступающий от нейрона А, является положительным, и от нейрона В ожидается положительный отклик, то связь между этими нейронами усиливается.

Проверим, как с помощью метода обучения Хебба с учителем можно научить сеть распознавать набор ассоциаций между образами. Ассоциации задаются как набор упорядоченных пар {<Х₁, Y₁>, <Х₂, Y₂>, …, <Х_t , Y_t>}, где X_i и Y_i - вектор ассоциируемых между собой образов. Предположим, размерность вектора X_i равна n, а размерность Y_i – m. Построим сеть, соответствующую этой ситуации. Она должна состоять из двух слоев, первый из которых содержит n нейронов, а второй – m (рис. 17).

Для обучения этой сети воспользуемся формулой настройки весов из предыдущего раздела

∆W = c*f ( X, W)*X,

где f(X,W) – реальный выход нейронной сети. При обучении с учителем заменим реальный выход нейронов ожидаемым выходным вектором D. Получим

∆W = c* D*X

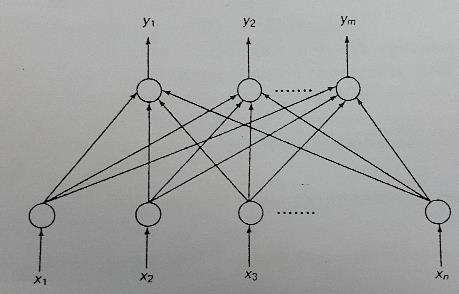
Рис. 17. Изучение ассоциаций с помощью метода обучения Хебба с учителем

Возьмем пару векторов <Х₁, Y₁> из набора ассоциаций и применим это правило обучения к узлу к выходного слоя

∆W_ik = c* d_k*x_i

где ∆W_ik – весовая добавка к связи нейрона i входного слоя с узлом к выходного слоя,

d_k – ожидаемый выход k-го нейрона,

х_i – i-й элемент вектора X.

Эта формула применяется для настройки всех весов связей всех нейронов выходного слоя. Вектор – это входной вектор X, a – выходной вектор Y. Применяя эту формулу для настройки отдельных весов связей с каждым нейроном выходного слоя, приходим к формуле модификации весов для всего выходного слоя

∆W = c* Y*X

где Y*X – внешнее векторное произведение, определяемое как матрица

.

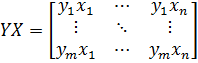Чтобы обучить сеть всему набору ассоциированных пар, нужно организовать итерационную процедуру настройки весов для каждой пары <Х_i,Y_i> по формуле

W^t+1=W^t+c Y*X.

Для всего обучающего множества имеем

W¹ = W⁰+c*(Y₁*X_l+ Y₂*Х₂+... + Y_t*Х_t) ,

где W⁰ – исходная конфигурация весов. Если исходные веса W⁰ инициализировать нулевым вектором <0;0;...;0>, а коэффициент обучения с выбрать равным 1, получим следующую формулу вычисления весов

W=Y₁*X₁+ Y₂*Х₂+...+ Y_t*Х_t.

Сеть, отображающая вектор входов в вектор выходов и обученная по этой формуле настройки весов, называется линейным ассоциатором. Как станет ясно впоследствии, такая модель позволяет хранить множество ассоциаций в матрице связей. Это приводит к возможности взаимодействия между сохраненными шаблонами. Проблемы, возникающие при таком взаимодействии, будут рассмотрены в следующих разделах.