Сеть Кохонена для изучения прототипов

Нейросетевой алгоритм кластеризации Кохонена "победитель забирает все" является алгоритмом решения задачи классификации с помощью персептрона.

В результате итерационного обучения персептрона формируется конфигурация весовых коэффициентов, которая обеспечивает линейное разделение двух классов. Линейная поверхность, определяемая этими весами, получается путем неявного вычисления центра каждого кластера в евклидовом пространстве. Этот центр кластера служит прототипом класса при решении задачи классификации с помощью персептрона.

Алгоритм обучения Кохонена не требует участия учителя. При таком обучении набор прототипов создается случайным образом и уточняется до тех пор, пока прототипы не обеспечат явного представления кластеров данных. В процессе работы алгоритма коэффициент скорости обучения постепенно уменьшается, чтобы каждый новый входной вектор оказывал все меньшее влияние на прототип.

На рис. 14 показана сеть Кохонена, предназначенная для классификации данных из табл. 4. Эти данные представлены в двухмерном декартовом пространстве, поэтому прототипы, представляющие кластеры данных, тоже являются упорядоченными парами. Для представления кластеров данных выбрано два прототипа - по одному на каждый кластер. Узлы А и В случайным образом инициализированы значениями (7,2) и (2,9). Случайная инициализация подходит только для таких простых примеров, как этот. Обычно в качестве начальных значений векторов весовых коэффициентов выбираются представители каждого кластера.

Вектор весовых коэффициентов нейрона-победителя является ближайшим к входному вектору. Этот вектор весов уточняется и становится еще ближе к входным данным, в то время как весовые коэффициенты остальных нейронов остаются неизменными. Благодаря явному вычислению евклидова расстояния от входного вектора до каждого из прототипов нет необходимости нормализовать эти векторы.

Классификация выполняется в контексте самоорганизации сети. Обычно при обучении сети методом Кохонена входные данные обрабатываются в случайном порядке, однако данные из табл. 4 будут выбираться сверху вниз. Сначала измеряется расстояние от точки (1,1) до каждого из прототипов

||(1 1) – (7 2)|| = (1–7)² + (1–2)² = 37,

||(1 1) – (2 9)|| = (1–2)² + (1–9)² = 65.

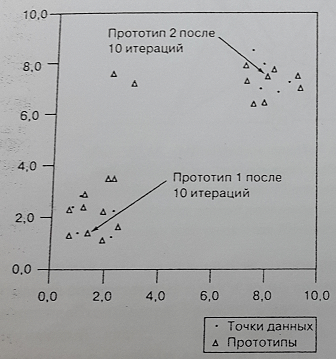
Рис. 13. Обучение сети Кохонена без учителя, при котором генерируется последовательность прототипов, представляющих классы из табл. 4

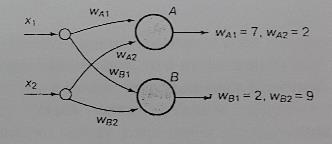
Рис. 14. Архитектура сети Кохонена для классификации данных из табл. 4

Узел А(7; 2) становится победителем, так как он ближе к точке (1; 1). Расстояние между этими точками – ||(1; 1) – (7; 2)||, причем квадратный корень вычислять нет необходимости, поскольку эта функция возрастающая. Теперь для узла-победителя нужно пересчитать значения весовых коэффициентов, установив коэффициент скорости обучения равным 0,5. На второй итерации

W² = W¹ + c(X¹–W¹) = (7; 2) +0,5((1; 1) – (7; 2)) =

= (7; 2) +0,5((1; –7),(1: –2)) = (7; 2) +(–3; –0,5) = (4; 1,5)

На второй итерации обучения вычислим расстояния от точки (9,4; 6,4):

||(9,4; 6,4) – (4; 1,5)|| = (9,4–4)² + (6,4–1,5)² = 53,17,

||(9,4; 6,4) – (2; 9)|| = (9,4–2)² + (6,4–9)² = 60,15.

Снова победителем является узел А. Веса связей перед третьей итерацией обучения составляют

W³ = W² + c(X²–W²) = (4; 1,5) +0,5((9,4; 6,4) – (4; 1,5)) =

= (4; 1,5) +(2,7; 2,5) = (6,7; 4).

На третьей итерации для точки (2,5; 2,1) имеем

||(2,5; 2,1) – (6,7; 4)|| = (2,5–6,7)² + (2,1–4)² = 21,25,

||(2,5; 2,1) – (2; 9)|| = (2,5–2)² + (2,1–9)² = 47,86.

Узел А снова становится победителем, и для него вычисляется новый весовой вектор. На рис. 13 показана эволюция прототипов в течение 10 итераций. Алгоритм генерации данных, представленных на рис. 13, выбирает очередные входные данные из табл. 4 случайным образом, поэтому эти точки отличаются от вычисленных выше. Как показано на рис. 13, в процессе обучения прототипы постепенно смещаются к центрам кластеров. Напомним, что обучение выполняется без учителя на основе алгоритма с подкреплением "победитель получает все". В процессе такого обучения строится последовательность явных прототипов, представляющих кластеры данных.