Последовательность выполнения нечеткого вывода

Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую

специалистами предметной области в виде совокупности нечетких правил сле-

дующего вида:

П₁: если x есть A₁, то y есть B₁;

П₂: если x есть A₂, то y есть B₂;

…

П_n: если x есть A_n, то y есть B_n,

где x– входная лингвистическая переменная (имя для известных значений данных); y – выходная лингвистическая переменная (имя для значения данных, которое будет вычислено); A_i, B_i – функции принадлежности (нечеткие подмножества), определенные соответственно на x и y; «x есть A» – нечеткое высказывание, называемое предпосылкой правила; «y есть B» – нечеткое высказывание, называемое заключением правила.

Пример подобного правила:

Если цена высокая, то спрос низкий.

Здесь цена – входная переменная x; спрос – выходное значение y; высокая, низкий – функции принадлежности (нечеткие подмножества), определенные на множествах значений цены и спроса соответственно.

В нечетких управляющих системах все правила работают одновременно, но степень их влияния на результат различна. Поэтому основой функциониро-

вания нечетких управляющих систем является вычисление обобщенного ре-

зультата, учитывающего влияние всех правил.

Процесс обработки нечетких правил вывода в управляющих системах состоит из четырех этапов:

1. Введение нечеткости (фазификация). Функции принадлежности, определенные на входных переменных, применяются к их фактическим значениям для определения степени истинности предпосылки каждого правила.

2. Нечеткий вывод. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям правил. Это дает нечеткое подмножество для переменной вывода каждого правила. В качестве правил логического вывода используются операции min (МИНИМУМ) или prod (ПРОИЗВЕДЕНИЕ). В логическом выводе МИНИМУМА функция принадлежности заключения правила «отсекается» по высоте, соответствующей вычисленной степени истинности предпосылки правила. В логическом выводе ПРОИЗВЕДЕНИЯ степень истинности предпосылки правила используется как коэффициент, на который умножаются значения функции принадлежности заключения правила.

3. Композиция. Все нечеткие подмножества, определенные для каждой переменной вывода (во всех правилах), объединяются вместе и формируют одно нечеткое подмножество для каждой переменной вывода. При таком объединении используется операция max (МАКСИМУМ) или sum (СУММА). При композиции МАКСИМУМ выполняется объединение функций принадлежности нечетких подмножеств 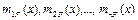по формуле:

,

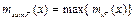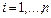
При композиции СУММА выполняется суммирование значений всех функций принадлежности по формуле:

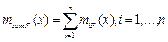
Скаляризация осуществляется различными способами. Чаще всего используется определение «центра тяжести» Н функции принадлежности нечеткого подмножества по формуле (7.4). Другой способ скаляризации – использование максимального значения функции принадлежности.