Понятие нечеткого числа
Одной из областей применение нечеткой логики является выполнение арифметических операций с нечеткими множествами. Для снижения трудоемкости таких операций используется специальный тип нечетких множеств – нечеткие числа.
Нечетким числом(НЧ) называется нечеткая переменная, имеющая следующие свойства: 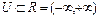 ;
; 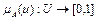 .
.
Другими словами, нечеткое число– именованное нечеткое множество, для которого универсальное множество U представляет собой интервал действительной оси R.
В реальных задачах используются кусочно-линейные нечеткие числа.Для упрощения арифметических операций кусочно-линейные функции принадлежности дополнительно аппроксимируют, чтобы получить специальный вид нечетких чисел – параметрические нечеткие числа или нечеткие числа
(L–R)–типа, которые характеризуются компактностью представления и просто-
той реализации арифметических операций.
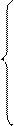 Нечеткое число А называется нечетким числом (L–R)–типа, если его функция принадлежности имеет следующий вид (рис. 7.8):
Нечеткое число А называется нечетким числом (L–R)–типа, если его функция принадлежности имеет следующий вид (рис. 7.8):
0, 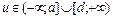
|
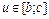 ,
,
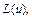
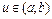
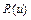 ,
, 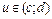
где 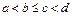 – параметры нечеткого числа; L(x), R(x) – некоторые функции.
– параметры нечеткого числа; L(x), R(x) – некоторые функции.
Нечеткое параметрическое число обозначается (a, b, c, d)LR.
Таким образом, нечеткое число (L–R)–типа описывается шестью параметрами: четырьмя числами, обозначающими его границы, и двумя функциями, определяющими форму его функции принадлежности.
 |
Рис.7.8 Параметрические нечеткие числа
Нечеткое числоназывается унимодальным, если оно имеет только одну точку, в которой функция принадлежности равна единице, т.е. его параметры b и c равны, в противном случае нечеткое число называется толерантным (см. рис. 7.8). Унимодальные нечеткие числа обозначаются пятью параметрами (a, b, d)LR.
В качестве LR–функций наиболее часто используют линейные зависимости, задаваемые следующими соотношениями:
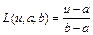 ,
, 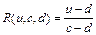 .
.
LR – функции также могут задаваться квадратичными, экспоненциальными и другими зависимостями.
В случае использования линейных функций унимодальные и толерантные нечеткие числа называют соответственно треугольными и трапециевидными и обозначают (a, b, d) и (a, b, c, d).
Для нечетких чисел особым образом определяется понятие знака и нулевого значения.
Нечеткое число А называется положительным, если его основание лежит в положительной действительной полуоси 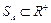 или
или
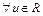 и
и 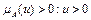 .
.
Нечеткое число А называется отрицательным, если его основание лежит в отрицательной действительной полуоси 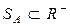 или
или
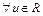 и
и 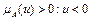 .
.
Для параметрических нечетких чисел знак определяется значениями параметров: положительное нечеткое число, если a > 0; отрицательное, если d < 0; нечеткий ноль, если 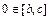 .
.
Дата добавления: 2016-04-22; просмотров: 2121;
