Операции с нечеткими числами

Одной из важнейших операций с нечеткими числами является их сравнение. Результат сравнения очевиден лишь в том случае, если основания сравниваемых нечетких чисел M и N не пересекаются, т.е 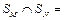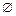. В этом случае большим считается то число, чье основание на действительной оси расположено правее (рис. 7.9).

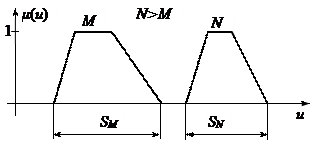Рис. 7.9 Сравнение НЧ с непересекающимися основаниями

Однако в большинстве случаев основания нечетких чисел пересекаются,

поэтому их сравнение происходит следующим образом. Для каждого из сравниваемых нечетких чисел M и N вычисляют специальные меры Н(М), Н(N), которые затем сравнивают:

.

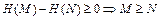Вычисление меры Н выполняется двумя способами:

- поиск точки максимума;

- поиск центра тяжести.

В случае поиска максимума величина Н является точкой на действительной оси, которая соответствует максимальному значению функции принадлежности (рис. 7.10). Используются три разновидности максимума: наибольший из максимумов (LOM), наименьший из максимумов (SOM) и центр максимумов (MOM).

Рис. 7.10 Сравнение по максимуму функций принадлежности

Центр тяжести нечеткого числа 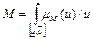вычисляется по формуле:

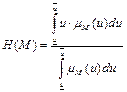. (7.4)

Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества.

Сравнение нечетких чисел более предпочтительно выполнять на основе поиска центра тяжести.

Еще одной важной операцией с нечеткими множествами, в том числе нечеткими числами, является определение меры сходства. Обычно данную операцию применяют для этого, чтобы определить какое из двух нечетких множеств больше похоже на третье. Прикладное значение такой операции заключается в следующем. При задании параметров некоторой системы могут использоваться лингвистические переменные, тогда значениями параметров являются нечеткие множества. Обработка и анализ параметров требует выполнения над ними некоторых преобразований, в результате которых также получаются нечеткие множества. Но представлять их в качестве результата нецелесообразно. Результат лучше представить с помощью лингвистических переменных. Чтобы выяснить, на какой из термов лингвистической переменной больше похож результат, и применяется процедура вычисления меры сходства. Терм, для которого она окажется максимальной, считается результатом.

Указанная процедура получила название лингвистической аппроксимации и служит средством обратного преобразования количественных данных в качественные.

Мера сходства для совпадающих нечетких множеств должна быть равна 1, а для непересекающихся – 0.

Общая формула для вычисления меры сходства двух нечетких множеств M и N имеет следующий вид:

,

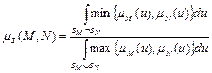где 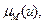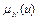– функции принадлежности нечетких множеств M и N;

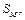
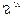– основания нечетких множеств M и N.

Данное выражение интерпретируется как отношение площадей функций принадлежности пересечения и объединения рассматриваемых нечетких множеств (рис. 7.11).

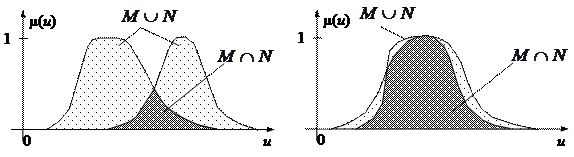Рис. 7.11 Графическое представление меры сходства НМ