Операции с нечеткими множествами

Подмножеством нечеткого множества А является нечеткое множество С, если выполняется условие:

Дополнением нечеткого множества А называется нечеткое множество D, имеющее функцию принадлежности .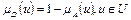

Объединением нечетких множеств А и С называется нечеткое множество 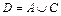, имеющее функцию принадлежности:

.

Пересечением нечетких множеств А и С называют нечеткое множество D = с функцией принадлежности .

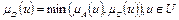Разностью нечетких множеств А и С называется нечеткое множество D = А \ С с функцией принадлежности .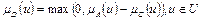

Декартовым произведением нечетких множеств 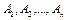универсальных множеств 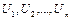называется нечеткое множество уни-

версального множества 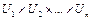, имеющее функцию принадлежности:

.

На рис. 7.3 проиллюстрированы некоторые из данных выше определений.

Для нечетких множеств также вводят специальные операции.

Суммой нечетких множеств А и C называется нечеткое множество 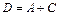, имеющее функцию принадлежности:

.

Скалярным произведением нечетких множеств А и С называют нечеткое множество 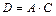, имеющее функцию принадлежности:

.

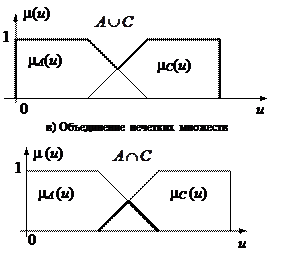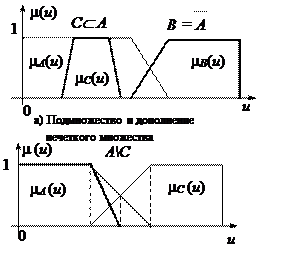б) Разность нечетких множеств г) Пересечение нечетких множеств

Рис. 7.3 Операции с нечеткими множествами

Степенью a нечеткого множества А называется нечеткое множество с функцией принадлежности .

Концентрированием нечеткого множества А называется нечеткое множество .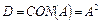

Расширением нечеткого множества А называется нечеткое множетво .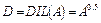

Операции концентрирования и расширения широко используются при работе с лингвистическими переменными.

Перечисленные специальные операции с нечеткими множествами проиллюстрированы на рис. 7.4.

		г) Расширение нечеткого множества