Понятие нечеткого множества

Значения лингвистической переменной определяются через так называемые нечеткие множества (НМ), которые в свою очередь определены на некотором базовом наборе значений или базовой числовой шкале, имеющей размерность. Каждое значение ЛП определяется, как нечеткое множество (например, НМ «низкий рост»).

Нечеткое множество определяется через некоторую базовую шкалу (универсальное множество U) и функцию принадлежности нечеткому множеству m( u ), u Î U, принимающую значения на интервале [0, 1]: m(х) Î [0,1]. Нечеткое множество определяет субъективную степень уверенности эксперта в принадлежности конкретного значения базовой шкалы данному нечеткому множеству.

Рассмотрим понятие «рост человека». В качестве универсального множества U можно использовать действительный интервал [0; 300], покрывающий любой возможный рост человека в см. Определим на этом универсальном множестве нечеткие множества «низкий рост» и «высокий рост». К людям с низким ростом принадлежат те, чей рост менее 150 см, а люди с ростом более 180 см однозначно относятся к высоким. В интервале от 150 см до 180 см рост человека можно отнести к низкому или высокому с той или иной степенью уверенности. Например, рост 170 см можно отнести к высокому с некоторой степенью принадлежности m₁, а к низкому – со степенью принадлежности m₂. В то время как рост в 140 см принадлежит нечеткому множеству «высокий рост» со степенью 0, а множеству «низкий рост» – со степенью 1.

Таким образом, для задания НМ необходимо определить:

1. универсальное множество U, которое содержит все рассматриваемые элементы;

2. множество значений степени принадлежности элементов из U нечеткому

множеству ([0,1]);

3. правило, определяющее состав нечеткого множества, т.е. правило, в соответствии с которым каждому элементу из множества U ставится в соответствие элемент из интервала [0,1].

Для дискретных универсальных множеств нечеткое множество представляет

собой совокупность пар {u_i, m( u_i)}, u_i Î U , m( u_i) Î [0,1], i = 1, 2, … , n,

где n – число элементов (мощность) множества U.

Для непрерывных универсальных множеств правило представляет собой аналитически заданное отображение: m_А: U ® [0,1].

Итак, нечетким множеством А универсального множества U называется отображение m_А: U ® [0,1], которое ставит в соответствие каждому элементу u множества U степень его принадлежности нечеткому множеству А и называется функцией принадлежности нечеткого множества А: m_А( u), u Î U.

Для задания нечеткого множества достаточно указать его функцию принадлежности m_А( u). Чтобы подчеркнуть дискретный или непрерывный характер нечеткого множества, используют соответственно записи со знаком суммы или интеграла: ; .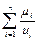

Нечеткое множество отличается от обычного множества набором возможных значений функции принадлежности. Если для обычного множества функция принадлежности принимает только два значения: 1 – если элемент принадлежит множеству, 0 – в противном случае, то функция принадлежности нечеткого множества принимает значения в интервале [0,1], т.е. элемент может принадлежать нечеткому множеству с некоторой степенью, меньшей 1.

Кроме понятия нечеткого множества в нечеткой логике также определены

еще несколько понятий и терминов.

Носителем (основанием) А называется подмножество универсального множества 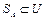, такое что > 0.

a-уровнем нечеткого подмножества А универсального множества U называется такое подмножество 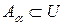, для которого верно: .

Будем считать, что основание нечеткого множества является его нулевым уровнем: .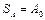

Высотой нечеткого множества А называется верхняя граница значений

его функции принадлежности: 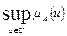. Если высота нечеткого множества

равна 1, то оно называется нормальным, если меньше 1 – субнормальным. Субнормальное нечеткое множество можно нормировать: .

На рис. 7.2 приведены нечеткие множества, иллюстрирующие пример с ростом человека и данные выше определения.

Рис. 7.2 Примеры нечетких множеств

Оба нечетких множества имеют высоту 1, т.е. являются нормальными. Основанием НМ «высокий рост» является интервал [150; 300], а НМ «низкий рост» – [0; 180] соответственно. Для последнего приведен также пример a-уровня.

Для обоих нечетких множеств аналитические выражения их функций принадлежности имеют следующий вид:

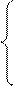
или 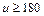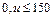или u > 300

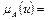
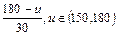
1,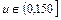

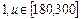
Теперь можно точно определить степень принадлежности того или иного значения нечеткому множеству. Например, рост 170 см можно отнести к высокому со степенью принадлежности 2/3, а к низкому – со степенью принадлежности 1/3. ( 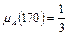, ). Таким образом, человек с таким ростом будет считаться скорее высоким, чем низким.

Функцию принадлежности нечеткого множества не следует путать с вероятностью, носящей объективный характер и подчиняющейся другим математическим зависимостям.