Вероятностный подход к представлению неопределенности

Одним из способов представления неопределенной информации является вероятностный подход. При этом одним из основных используемых понятий является условная вероятность.

Условная вероятность события d при данном s – это вероятность наступления события d при условии, что наступило событие s, например, вероятность того, что пациент страдает заболеванием d, если у него обнаружен симптом s.

В теории вероятностей для вычисления условной вероятности события d при данном s используется следующая формула:

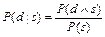(7.1)

Условная вероятность представляет собой отношение вероятности совпадения событий d и s к вероятности появления события s. Из формулы (7.1) следует:

.

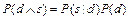Если разделить обе части последнего выражения на 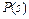и подставить в (7.1), получим правило Байеса в простейшем виде:

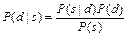(7.2)

Это правило позволяет определить вероятность 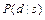через известную условную вероятность 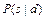. В полученном выражении - априорная вероятность наступления события d, а 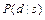- апостериорная вероятность, т.е. вероятность того, что событие d произойдет, если известно, что событие s свершилось.

Формула (7.2) более удобна для практических приложений, чем формула (7.1).

Предположим, что у пациента имеется некоторый симптом заболевания,

например, боль в груди, и надо узнать, какова вероятность того, что этот симптом

является следствием определенного заболевания, например, инфаркта миокарда. Для того, чтобы вычислить вероятность Р ( инфаркт миокарда | боль в груди ) по формуле (7.1), нужно знать (или оценить каким-либо способом), сколько человек в мире жалуются на боль в груди и сколько человек и болеют инфарктом миокарда, и жалуются на боль в груди. Как правило, такая информация отсутствует. Таким образом формула (7.1) на практике не применима.

В теории вероятностей понятие вероятности определяется как объективная частотность (частота появления события при достаточно продолжительных независимых испытаниях). Однако, с точки зрения практических приложений более применим субъективистский подход к понятию вероятности, позволяющий иметь дело с оценками частоты появления событий, а не с действительной частотой.

Например, врач может не знать или не иметь возможности вычислить, какая часть пациентов, жалующихся на боль в груди, страдает инфарктом миокарда, но на основании собственного опыта он может оценить, у какой части его пациентов, страдающих этим заболеванием, встречался такой симптом. Следовательно, он может оценить значение вероятности Р ( боль в груди | инфаркт миокарда ), т.е. вероятности , где s означает симптом, а d – заболевание. Тогда по формуле (7.2) можно вычислить вероятность 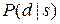. Оценку вероятности можно взять из публикуемой медицинской статистики, а оценить значение 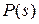врач может на основании собственных наблюдений.

Вычисление 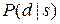не вызывает затруднений, если речь идет о единственном симптоме. Допустим, имеется множество заболеваний D и множество симптомов S, причем для каждого элемента из D нужно вычислить условную вероятность того, что у пациентов, страдающих этим заболеванием, наблюдался один определенный симптом из множества S. Если в множестве D имеется m элементов, а в множестве S – n элементов, потребуется вычислить 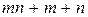оценок вероятностей.

Но вычисления значительно усложняются, если в процесс установления диагноза включить не один симптом, а несколько.

В более общей форме правило Байеса имеет вид:

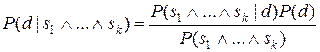(7.3)

и требует вычисления оценок вероятностей, поскольку в общем случае для вычисления 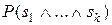нужно вычислить произведения вида

.

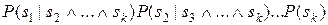Однако, если предположить, что некоторые симптомы независимы друг от друга, объем вычислений существенно снижается. Независимость любой пары симптомов s_i и s_j означает, что 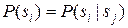, из чего следует соотношение .

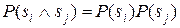Если все симптомы независимы, то объем вычислений будет таким же, как и в случае учета при диагнозе единственного симптома.

В большинстве случаев можно предположить наличие условной независимости. Это означает, что пара симптомов s_i и s_j является независимой на основании какого-либо дополнительного свидетельства или фундаментальных знаний Е. Таким образом, .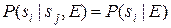

Например, если в автомобиле нет горючего и не работает освещение, то на основании знаний об устройстве автомобиля можно считать эти симптомы независимыми. Но если автомобиль не заводится и не работает освещение, то заявлять, что эти симптомы независимы нельзя, поскольку они могут быть следствием одной и той же неисправности аккумуляторной батареи. Необходимость отслеживать такого рода связи значительно увеличивает объем вычислений в общем случае.

Таким образом, использование вероятностного подхода заставляет выбирать одно из двух:

- либо предположить независимость данных и использовать менее трудоемкие методы вычислений, следствием чего будет снижение достоверности результатов;

- либо отслеживать зависимость между используемыми данными, количественно оценить эту зависимость, т.е. усложнить вычисления, но получить более достоверные результаты.

Вероятностный подход для представления неопределенности информации характеризуется следующими недостатками:

- назначение вероятности определенным событиям требует информации, которой мы не располагаем;

- неясно, как количественно оценивать часто встречающиеся на практике качественные характеристики и понятия, такие как «в большинстве случаев», «в редких случаях», «низкий», «высокий»;

- обновление вероятностных оценок требует большого объема вычислений.

Указанные трудности использования вероятностного подхода породили новый формальный аппарат для работы с неопределенной информацией, который получил название нечеткая логика (fuzzy logic). Этот аппарат широко используется при решении задач искусственного интеллекта.

Лекция. Нечеткие множества

При решении задач человек в некоторых случаях оперирует качественными характеристиками объектов (много, мало, сильный, слабый и т.п.). Эти характеристики размыты и не могут быть однозначно интерпретированы, но содержат важную информацию для принятия решений.

Кроме того, часто используются неточные знания, которые не могут рассматриваться как полностью истинные или ложные. Достоверность их характеризуется промежуточной величиной (от 0 до 1). Для формального представления подобной информации разработан аппарат нечёткой логики (fuzzy logic). В дальнейшем данное направление искусственного интеллекта получило название мягкие вычисления (soft computing).

Основное понятие в нечеткой логике – понятие лингвистической переменной.

Лингвистическая переменная (ЛП) – это переменная, значения которой определяются набором вербальных (словесных) характеристик некоторого свойства. Например, ЛП «рост» определяется через набор {карликовый, низкий, средний, высокий}.