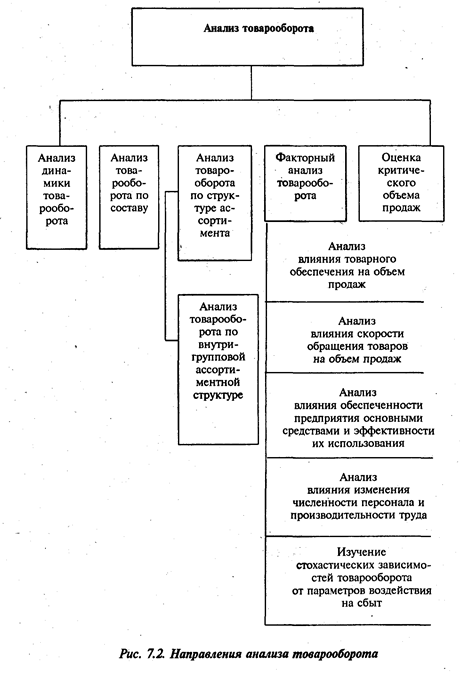
Анализ динамики товарооборота
В оценке и анализе развития товарооборота используются различные методы исследования динамических процессов: построение динамических рядов (в натуральных и стоимостных единицах), расчет показателей динамики (базисных и цепных темпов роста и прироста, абсолютных приростов), построение трендовых регрессионных моделей динамики, индексный метод.
Изменение уровней рядов динамики происходит под влиянием множества факторов, которые по-разному влияют на изменение товарооборота, — это могут быть факторы как внешние, так и внутренние. Одни факторы оказывают постоянное влияние на товарооборот и формируют основную тенденцию (тренд). Например, инфляция оказывает влияние на увеличение товарооборота в стоимостных показателях и в результате действия того же фактора происходит снижение физического товарооборота; рост денежных доходов населения приводит к устойчивому росту объема продаж.
Другие факторы имеют непостоянное или случайное действие. Например, увеличение площади торгового зала приводит к росту товарооборота. Действие таких факторов вызывает единоразовое увеличение объема продаж.
Различие действия постоянных, периодических и разовых причин обусловливает необходимость изучения основных компонентов рядов динамики:
• тренда;
• периодических колебаний;
• случайных отклонений.
При выявлении тренда розничного товарооборота решаются две задачи:
1) качественная характеристика тренда, может быть дана с помощью визуальной оценки эмпирических данных или графика;
2) измерение выявленного тренда, т. е. получение обобщающей количественной оценки основной тенденции.
Наиболее распространенные методы изучения тренда:
• укрупнение интервалов;
• сглаживание скользящей средней;
• аналитическое выравнивание.
Метод укрупненных интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Главное в этом методе — преобразование первоначального ряда динамики в ряды более продолжительных периодов (месячные — в квартальные, квартальные — в годовые). В результате укрупнения интервалов общая тенденция роста продажи становится очевидной.
Сущность сглаживания методом скользящей средней состоит в том, что по исходным уровням ряда (эмпирическим данным) определяют расчетные (теоретические) уровни, в которых случайные тенденции погашаются, а основная тенденция развития выражается в виде некоторой плавной линии. Для выражения общей тенденции развития этим методом прежде всего устанавливаются ее звенья. Звенья скользящей средней должны составляться из числа уровней, отвечающих длительности внутригодовых циклов в изучаемом явлении. Для ряда динамики, отражающего развитие товарооборота по кварталам, скользящие средние обычно составляются из четырехзначных звеньев. Их расчет состоит в определении средних величин из 4-уровневого ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:

Для определения сглаженных уровней производится центрирование. При применении метода скользящей средней к ряду динамики месячных уровней рассчитывается 12-членная скользящая средняя.
Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания.
Для измерения тренда используется метод аналитического выравнивания. Основным содержанием его является то, что основная тенденция развития у, рассчитывается как функция времени уti = f (ti). Определение теоретических уровней уti производится на основе так называемой адекватной математической функции. Адекватная функция подбирается методом наименьших квадратов — по минимальному отклонению суммы квадратов между теоретическими и эмпирическими уровнями товарооборота, т. е.
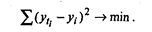
Важнейшую проблему составляет подбор математической функции, по которой рассчитываются теоретические уровни тренда. В практике изучения тренда различают следующие эталонные типы развития товарооборота во времени, в основе которых лежат абсолютные приросты, относительные приросты и темпы роста:
1. Равномерное развитие — линейная форма тренда применяется для рядов динамики со стабильными цепными абсолютными приростами (Δуц ≈ const). Основная тенденция развития отображается уравнением прямолинейной функции: уt = a0 + a1t. Параметр а1 является коэффициентом регрессии, определяющим направление развития. Если а1 > 0, то уровни ряда динамики возрастают, если a 1 < 0 - равномерно снижаются;
2. Равноускоренное (равнозамедленное) развитие - параболическая форма тренда - применяется для рядов динамики со стабильными темпами прироста (Tпр ≈ const). Основная тенденция развития отображается функцией параболы второго порядка:
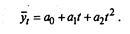
Параметр a2 характеризует постоянное изменение интенсивности развития (в единицу времени). При a2 > 0 происходит ускорение развития, а при a2 < 0 идет процесс замедления роста;
3. Развитие с переменным ускорением (замедлением) отображает функция параболы 3-го порядка;
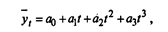
где а3 отображает изменение ускорения (при а3 > 0 - ускорение возрастает, при а3 < 0 — ускорение замедляется).
4. Развитие по экспоненте. Экспоненциальное сглаживание временных рядов - модификация метода наименьших квадратов для анализа временных рядов, при котором более поздним наблюдениям придается больший вес, иными словами, веса точек ряда убывают (экспоненциальный закон) по мере удаления в прошлое.
Этот тип динамики характеризуют стабильные темпы роста
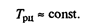
Основная тенденция в рядах динамики с постоянными темпами роста отображается показательной функцией
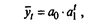
где а1 — темп роста (снижения) изучаемого явления в единицу времени, т. е. интенсивность развития;
5. Развитие с замедлением роста в конце периода. У этого типа рядов динамики показатель цепного абсолютного прироста сокращается в конечных уровнях ряда динамики Δyц → 0 (достижение насыщения).
Основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией:
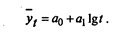
Практика статистического изучения тренда социально-экономических явлений показывает, что часто невозможно однозначно решить вопрос, какому виду развития больше всего отвечают показатели динамики. Реальные условия формирования показателей товарооборота предполагают изменение товарооборота под влиянием множества факторов разнонаправленного действия, поэтому трудно найти адекватную форму связи.
Для подтверждения гипотезы о возможном типе развития можно использовать графический метод. Наглядное изображение тренда можно получить по расположению на поле графика эмпирических уровней. Но график не может дать обобщенную оценку выявленного тренда.
Для определения параметров математических функций при анализе тренда используется способ отсчета времени от условного начала. Он основан на обозначении в ряду динамики показателей времени таким образом, чтобы 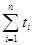 = 0. При этом в ряду динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевое значение и принимают его за условное начало отсчета времени, " + " — для всех последующих уровней и " -" — для предыдущих.
= 0. При этом в ряду динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевое значение и принимают его за условное начало отсчета времени, " + " — для всех последующих уровней и " -" — для предыдущих.
Тогда параметры уравнений определяются по формулам:
а) для прямолинейной функции
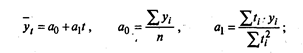
б) для показательной функции
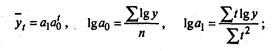
в) для параболы 2-го порядка

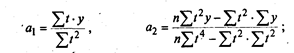
г) для параболы 3-го порядка
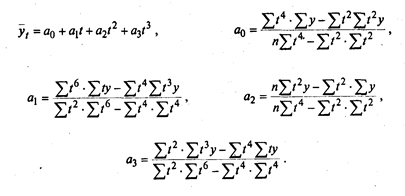
Дата добавления: 2016-02-11; просмотров: 2173;
