Расчет среднеквадратичного отклонения (другой вид формулы).
По определению среднее квадратичное отклонение равно (см. формулы 12,13)
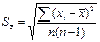
Числитель под корнем можно преобразовать:
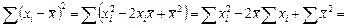
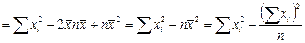
Следовательно, среднеквадратичную погрешность можно записать в виде:
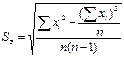
При использовании этой формулы алгоритм вычисления погрешности при прямых измерениях упрощается.
| xi | xi2 | 1. 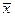 = = 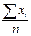 2.
2. 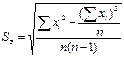 3.
3.  4.
4. 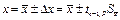 . .
|
| x1 | x12 | |
| x2 | x22 | |
| x3 | x32 | |
| ….. | ||
| xn | xn2 | |
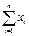
| 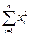
|
Однако следует иметь в виду, что в эту формулу входит малая разность, поэтому расчет необходимо производить с большим числом значащих цифр. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, то надежнее использовать алгоритм, предложенный в главе 5 §1.
Алгоритм вычисления среднеквадратичного отклонения при прямых измерениях высокой точности
| xi | xi-А | (xi-А)2 | 1. 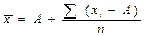 2.
2. 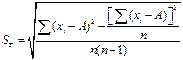 3.
3.  4.
4. 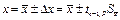 . .
|
| x1 | x1-А | (x1-А)2 | |
| x2 | x2-А | (x2-А)2 | |
| ….. | ….. | ….. | |
| xn | xn-А | (xn-А)2 | |
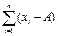
| 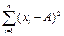
|
Здесь А – число близкое к 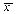 , см § 3.
, см § 3.
Дата добавления: 2016-04-19; просмотров: 677;
