Вычисление суммарной - случайной и систематической погрешности.
Если отношение неисключенной систематической погрешности измерения к случайной погрешности удовлетворяет неравенству:
0,8< 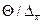 < 5 (41),
< 5 (41),
то границы погрешности результата измерений (общие доверительные границы) вычисляют с учетом и случайных и не исключенных систематических погрешностей, рассматриваемых как случайные величины.
При работе в лаборатории рекомендуется использовать следующий вариант расчета:
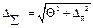
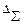 – оценка суммарного среднеквадратичного отклонения результата измерения.
– оценка суммарного среднеквадратичного отклонения результата измерения.
Θ – приборная (не исключенная систематическая) погрешность результата измерения
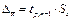 – доверительные границы случайной погрешности.
– доверительные границы случайной погрешности.
Пример.
Рассмотрим предыдущий пример измерения сопротивления нагрузки путем измерения падения напряжения на ней и тока в цепи.
Пусть были произведены пять измерений напряжения и тока в цепи. И каждый раз были получены различные значения напряжения и тока. Необходимо сопоставить не исключенную систематическую погрешность 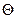 со случайной погрешностью
со случайной погрешностью 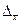 .
.
Полученные значения записаны в таблице.
Таблица 7
| Измеряемая величина | Результаты измерений | Средние значения | ||||
| U В | 500/5 = 100 | |||||
| I А | 5,00 | 4,95 | 4,90 | 5,10 | 5,00 | 24,95/ 5= 4,99 |
По алгоритму прямых измерений вычисляются доверительные границы напряжения и тока для доверительной вероятности P=0,95, а также их средние значения, считая, что погрешности этих величин обусловлены случайными ошибками. Получаем следующие значения:
SI =0,033166 ΔI = 3,2×0,033= 0,11
SU = 0,447 ΔU = 3,2×0,447= 1,43
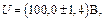
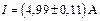 .
.
Суммарная средняя квадратичная погрешность сопротивления нагрузки будет определяться по формуле переноса ошибок:
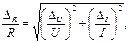
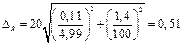


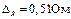 при P=0,95.
при P=0,95.
Приборная погрешность для такого же примера была рассчитана в предыдущем параграфе: 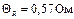
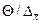 =0,57/0,51 = 1,1 – следовательно, необходимо учитывать и ту и другую погрешность.
=0,57/0,51 = 1,1 – следовательно, необходимо учитывать и ту и другую погрешность.
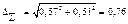
И окончательный результат будет записан в виде
R = (20,0 ± 0,8 Р=0,95) Oм
Дата добавления: 2016-04-19; просмотров: 1007;
