Учет погрешности приборов.

Если при измерении какой-либо величины при помощи физического прибора получают одно и то же значение при многократных измерениях, это не значит, что случайные погрешности определения этой величины равны нулю. Из этого факта будет следовать только то, что случайные погрешности при этих измерениях меньше систематических погрешностей, даваемых измерительными приборами, которые могут быть оценены по классу точности прибора. Приборная погрешность может быть указана или на самом приборе, или в его паспорте. В случаях, когда отсутствует паспорт прибора и не указан класс точности, приборную погрешность принято считать равной половине наименьшего деления шкалы прибора (половине цены деления шкалы)

При косвенных измерениях приборная (неисключенная систематическая) погрешность функции 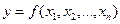будет определяться (см. ф 20) через приборные погрешности аргументов по формуле:

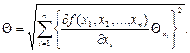(40)

Здесь Θ – приборная погрешность функции y, Θx_i - приборная погрешность величины x_i

Пример.

Предположим, что измеряется сопротивление нагрузки путем измерения падения напряжения на ней и тока в цепи. Произведено пять измерений падения напряжения и пять измерений тока, которые дали совершенно одинаковые результаты. Измеренный ток I=5 A, напряжение 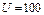В

Искомое сопротивление равно .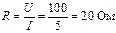

Так как случайные погрешности не наблюдались, будем оценивать не исключенную систематическую погрешность, обусловленную предельной погрешностью измерительных приборов, используемых в эксперименте (классом точности).

Напряжение измеряется вольтметром, предел измерения которого равен 200 В, а класс точности γ_кл.т.=1,0. Относительная погрешность напряжения будет определена по формуле 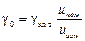и численно равна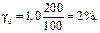

тогда предельная абсолютная погрешность напряжения .

Ток в цепи измеряется амперметром, его предел измерения –10 А, класс – 1,0. Относительная погрешность измерения тока

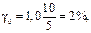
а абсолютная величина предельной погрешности тока 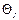=0,1 А

Функция 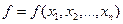имеет вид 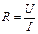, т.е. представляет собой частное двух аргументов. Воспользовавшись формулой 24, получим выражение для вычисления относительной погрешности сопротивления:

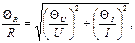
Тогда неисключенная систематическая погрешность сопротивления нагрузки

;

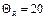
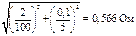Окончательный результат измерения сопротивления будет записан в виде

R = (20,0 ± 0,6) Oм