Некоторые сведения о неравноточных измерениях.

Бывают случаи, когда одну и ту же физическую величину измеряют несколько раз, но не в одинаковых условиях, а с разной степенью точности. Например, определение длины волны спектральной линии по положению дифракционных максимумов разных порядков.

В этом случае в качестве оценки значения искомой величины принимается средне взвешенное ее значение, вычисляемое по формуле:

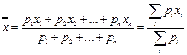, (38)

Здесь Р_i - вес соответствующей реализации, то есть некоторый коэффициент, зависящий от точности i-того измерения. Подбор этих коэффициентов задача в общем случае не простая. Обычно их выбирают обратно пропорционально квадратам относительных ошибок, соответствующих реализаций. Дисперсия средневзвешенного значения рассчитывается по формуле:

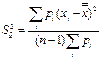(39)

Пример

Условиеобразования дифракционного максимума: d sinj = ± kl, где k = 0,1,2,... – порядок спектра, d – постоянная решетки, а j - угол дифракции. Следовательно, длину волны lможно определить, измерив углы j для разных k:

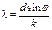
Поскольку постоянная решетки известна с большой степенью точности (ее погрешностью можно пренебречь), а порядок спектра – целое число, тогда погрешность длины волны будет определяться только погрешностью определения величины угла. Очевидно, что чем больше угол (больше порядок спектра), тем меньше будет относительная погрешность измерения угла (т.к. абсолютная погрешность прибора одинакова). Воспользовавшись формулой (17), можно получить:

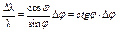
Пусть в процессе измерений получены следующие значения углов:

При k=1 φ₁=1⁰15׳ ctg φ₁= 45,8

k=2 φ₂=2⁰30׳ ctg φ₂= 22,9

k=3 φ₃=3⁰42׳ ctg φ₃= 15,5.

Таким образом, относительные ошибки в первом, втором и третьем порядках относятся как 3:2:1. Следовательно, веса следует выбирать: Р₁=1, Р₂=4, Р₃=9. Постоянная решетки d=0,002см.

Получаем:

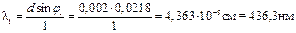
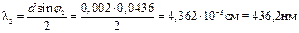
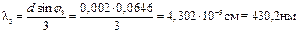
Тогда средневзвешенное значение будет равно:

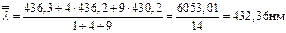
Дисперсия среднего взвешенного:

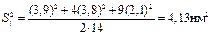
S_λ =2,03нм Δλ= S_λ ×t_p,n-1 =2,03×4,3= 8,7нм

Окончательный результат имеет вид λ= (432 ±9) нм