Обработка косвенных измерений. Функция одной переменной. (Формулы переноса ошибок).
Пусть искомая физическая величина Y является функцией измеряемой величины x.
Y =f(x)
Так как величина x не может быть определена абсолютно точно, то и рассчитанное значение Y будет содержать погрешность. Значение искомой функции следует находить, как функцию среднего арифметического значения измеренной величины 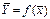 , то есть в формулу для ее определения подставить вычисленное среднее значение
, то есть в формулу для ее определения подставить вычисленное среднее значение 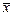
Как определить погрешность функции, если известна погрешность аргумента?
Для этого пользуются известным соотношением между дифференциалом функции df(x)и бесконечно малым приращением аргумента dx:
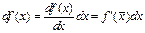
Полагая Dx»dx, а DY»dY , получаем выражение для погрешности функции:
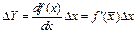
| (17) |
где Dx =tp,n-1 Sx , 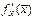 - производная функции
- производная функции 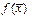 при x =
при x = 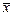 .
.
Иногда оказывается удобнее (проще) вычислить сначала относительную погрешность, а уже зная ее, определить доверительный интервал. Учитывая то, что: 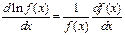 легко видеть, что относительную погрешность функции можно вычислить, воспользовавшись следующей формулой:
легко видеть, что относительную погрешность функции можно вычислить, воспользовавшись следующей формулой:
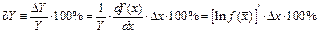
| (18) |
§ 3 Обработка косвенных измерений. Функция многих переменных. (Формулы переноса ошибок)
В общем случае искомая физическая величина может быть функцией не одной, а нескольких измеряемых величин, то есть: Y= f(X1, X2,…Xn)* Каждая из величин X1, X2,…Xn определяется с соответствующей погрешностьюDX1, DX2,… DXn. В этом случае средняя квадратичная погрешность функции будет равна корню квадратному из суммы квадратов частных производных функции по всем независимым переменным, домноженным на среднеквадратичную погрешность соответствующей величины:
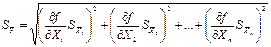
| (19) |
В данной формуле каждая скобка под корнем представляет собой вклад погрешности соответствующей величины в погрешность функции. Если погрешности различных измеряемых величин определены с одной и той же доверительной вероятностью, то формулу можно переписать в следующем виде:
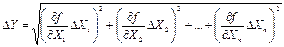
| (20) |
Относительная погрешность функции может быть вычислена по формуле:
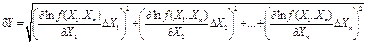
| (21) |
Приведенные формулы справедливы для любых функциональных зависимостей, однако, они довольно громоздки, производить по ним расчеты бывает достаточно сложно, они требуют больших затрат времени. В некоторых случаях бывает удобнее использовать выражения, преобразованные для частных случаев функциональной зависимости. Рассмотрим несколько таких частных случаев.
Погрешность алгебраической суммы
Пусть функция имеет вид:
Y = 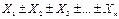 , тогда среднеквадратичная погрешность такой функции будет определяться:
, тогда среднеквадратичная погрешность такой функции будет определяться:
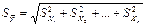
| (22) |
а выборочная дисперсия:
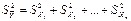
| (23) |
То есть выборочная дисперсия алгебраической суммы равна суммевыборочных дисперсий отдельных независимых переменных. Обратите внимание,на то, что в выражение для выборочной дисперсии функции все слагаемые входят со знаком «+», независимо от того, с каким знаком соответствующая величина входила в алгебраическую сумму.
Погрешность произведения.
Пусть функция имеет вид:
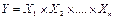 или
или 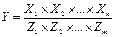
В этих случаях, воспользовавшись формулой (21) и, учитывая то, что логарифм произведения равен сумме логарифмов, получаем выражение для относительной погрешности функции:
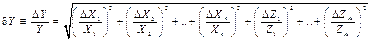
| (24) |
То есть относительная погрешность произведения (и частного) равна корню квадратному из суммы квадратов относительных погрешностей всех сомножителей. Также как и в случае суммы, обратите внимание, на то, что все слагаемые под корнем берутся со знаком «+», независимо от того в числитель или знаменатель выражения функции они входили.
Производить расчет по этой формуле обычно гораздо проще, чем по формуле (19), а доверительный интервал искомой величины легко найти:  .
.
Погрешности некоторых элементарных функций.
1. 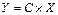 , где С=const;
, где С=const; 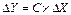
2. 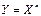 ;
; 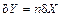
3. 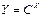 ;
; 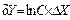
Дата добавления: 2016-04-19; просмотров: 1331;
