Практические способы расчета случайных погрешностей
Математическая обработка результатов измерений является весьма трудоемким делом, зачастую отнимающим больше времени, чем сами измерения. Она требует внимания и аккуратности. Задача упрощается, если пользоваться соответствующими алгоритмами, которые представляют собой план рациональной последовательности действий при нахождении результата и его погрешности.
Обработка прямых измерений (алгоритм прямых измерений).
Пусть искомая величина x измерена n раз, для нахождения 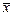 и
и 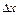 , рекомендуется записать данные в следующую таблицу и производить расчеты в указанном порядке.
, рекомендуется записать данные в следующую таблицу и производить расчеты в указанном порядке.
Таблица 1
| № | xi | xi - 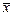
| (xi - 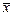 )2 )2
|
| x1 | x1 - 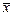
| (x1 - 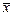 )2 )2
| |
| x2 | x2 - 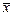
| (x2 - 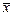 )2 )2
| |
| x3 | x3 - 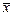
| (x3 - 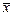 )2 )2
| |
| … | ….. | …… | ………. |
| n | xn | xn - 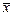
| (xn -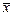 )2 )2
|
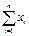
| 
|
1. Найти сумму всех xi ( 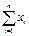 )
)
2. Найти 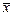 =
= 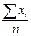
3. Заполнить третий и четвертый столбцы таблицы.
4. Сосчитать сумму в четвертом столбце 
5. Рассчитать среднеквадратичную погрешность среднего арифметического, используя полученную в четвертом столбце сумму. 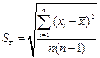
6. Найти в «таблице коэффициентов Стьюдента» tn-1,P для данного числа измерений и выбранной вероятности.
7. Определить 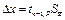
8. Записать окончательный результат 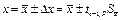 .
.
Пример. Пять раз измерен диаметр проволоки с помощью микрометра. Получены следующие результаты (столбец 2).
Таблица 2
| № | di, мм | di- 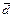 ,мм ,мм
| (di- 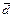 )2, )2,
|
| 3,90 | 0,01 | 1 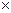 10-4 10-4
| |
| 3,85 | -0,06 | 36 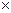 10-4 10-4
| |
| 3,88 | -0,03 | 9 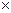 10-4 10-4
| |
| 3,97 | 0,06 | 36 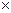 10-4 10-4
| |
| 3,95 | 0,04 | 16 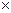 10-4 10-4
| |
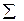
| 19,55 | 98 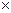 10-4 10-4
|
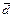 =19,55 / 5 =3,910 мм
=19,55 / 5 =3,910 мм
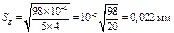
Для доверительной вероятности Р=0,95 и числа измерений n=5, коэффициент Стьюдента 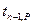 =3,2, тогда
=3,2, тогда
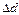 =3,2
=3,2 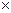 0,022= 0,070 мм.
0,022= 0,070 мм.
Окончательный результат: 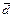 = (3,91±0,07 P=0,95 ) мм.
= (3,91±0,07 P=0,95 ) мм.
Относительная погрешность dd = (0,07 / 3,91) 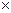 100% = 1,8%.
100% = 1,8%.
Возможны другие способы расчета, смотри приложение §§ 4,5.
Дата добавления: 2016-04-19; просмотров: 548;
