Распределение Стьюдента. На практике мы никогда не имеем дело с бесконечным числом измерений и не можем, следовательно, определить точно ни значение σ
На практике мы никогда не имеем дело с бесконечным числом измерений и не можем, следовательно, определить точно ни значение σ, ни значение х0.
В качестве оценки значения математического ожидания для выборки из n реализаций принято рассматривать их среднее арифметическое значение:
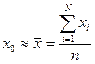
В качестве оценки дисперсии вводится величина выборочной дисперсии 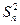 и величина выборочного среднеквадратичного отклонения
и величина выборочного среднеквадратичного отклонения 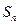 , определяемые:
, определяемые:
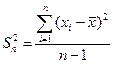 и и 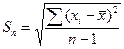
| (12) |
Можно показать, что при стремлении n к бесконечности 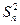 → σ2.
→ σ2.
Очевидно, что среднее арифметическое значение всех реализаций отличается от х0 меньше чем отдельное значение. Другими словами дисперсия ( 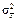 ) и среднеквадратичное отклонение (
) и среднеквадратичное отклонение ( 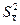 ) среднего арифметического меньше чем дисперсия и среднеквадратичное отклонение отдельного измерения. В теории вероятности доказываются следующие соотношения:
) среднего арифметического меньше чем дисперсия и среднеквадратичное отклонение отдельного измерения. В теории вероятности доказываются следующие соотношения:
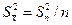 и и 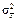 = σ2 /n = σ2 /n
| (13) |
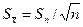 и и 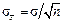
| (14) |
Если мы имеем дело с конечным (и обычно не очень большим) числом измерений, то распределение уже не является Гауссовым. Качественно характер распределения подобен нормальному, но описывается другой функцией плотности распределения вероятности и носит название - распределение Стьюдента (псевдоним английского математика В. Госсета).
Распределение Стьюдента, в отличие от Гауссова, не определяется однозначно дисперсией и средним значением реализаций, а зависит еще от числа измерений n. В распределение Стьюдента входит параметр t , называемый коэффициентом Стьюдента, он зависит от двух величин – от числа измерений и от доверительной вероятности, поэтому указывается с двумя индексами: tp,n . Таблица наиболее часто используемых коэффициентов Стьюдента приведена в приложении (§1). Коэффициент Стьюдента связывает среднеквадратичную ошибку среднего арифметического с величиной доверительного интервала.
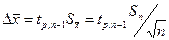
| (15) |
Чем больше требуемая вероятность, тем больше коэффициент Стьюдента и, следовательно, больше доверительный интервал. С увеличением числа измерений значение коэффициента Стьюдента убывает.
Окончательный результат представляют в виде:
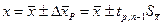
| (16) |
Как следует из сказанного, увеличение числа измерений необходимо для увеличения точности результатов. С ростом n среднее арифметическое ближе к истинному значению х0 и доверительный интервал Δх при заданной вероятности Р будет меньше.
Однако не следует забывать о существовании помимо случайных погрешностей еще и неисключенных систематических. Большое число измерений уменьшает только случайную ошибку, но, учитывая наличие систематической погрешности, проводить слишком большое число измерений нерационально.
Дата добавления: 2016-04-19; просмотров: 530;
