Распределение Стьюдента. Распределение Стьюдента (впервые получено английским математиком В

Распределение Стьюдента (впервые получено английским математиком В. Госсетом в 1908 г, который печатал свои работы под псевдонимом Стьюдент) выражается формулой

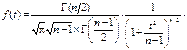
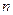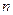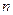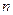где - число измерений, t – коэффициент Стьюдента, Г( ) –гамма-функция, представляющая обобщенное понятие факториала ( для целых чисел Г( +1)= ! Для полуцелых 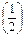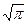– Г = , Г 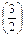= 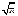/2 и т.д.

Кривые функции имеют такой же вид, как и кривые 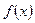распределения Гаусса (см. рис.2).

При n→∞ (практически уже при n>20) распределение Стьюдента переходит в нормальное распределение Гаусса с единичной дисперсией ( 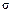=1).

Вычисление среднего арифметического при измерениях высокой точности

Вычисление среднего арифметического

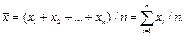
Если выбрать значение близкое к 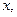тогда эту формулу можно записать в виде

=

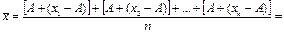
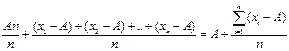
Данная формула оказывается более удобной, чем первая тогда, когда численное значение измеряемых величин имеют несколько значащих цифр. В этом случае приходится находить среднее арифметическое небольших разностей, а не самих больших чисел