Вероятность попадания случайной величины на заданный участок.
Пусть случайная непрерывная величина X может принять частное значение в интервале 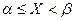 , причем известна ее функция распределения F(x). Требуется найти вероятность попадания ее в этот интервал, т.е.
, причем известна ее функция распределения F(x). Требуется найти вероятность попадания ее в этот интервал, т.е. 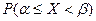 .
.
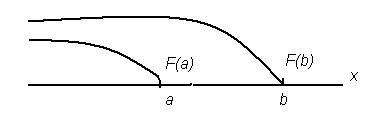
Рисунок 4 Определение значений функции распределения на границах интервала
По определению значение функции распределения F(b) в точке b является вероятностью того, что случайная величина примет значение меньшее b, а значение функции распределения F(a) в точке a - вероятностью того, что случайная величина примет значение меньшее a. Следовательно, вероятность попадания случайной величины в этот интервал будет определяться разностью значений функций распределения в граничных точках, т.е.
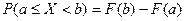 . (2.1)
. (2.1)
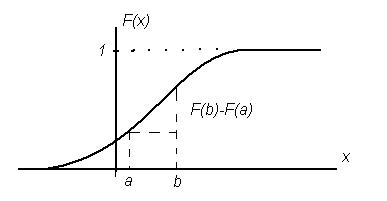
Рисунок 5 Определение 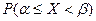 по функции распределения
по функции распределения
Вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке (рис. 5).
Пример 1: Прибор рассчитан на входное напряжение не большее 220 Вольт, а напряжение сети является случайной величиной с функцией распределения
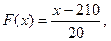 если 210<X<230;
если 210<X<230;
F(x) =0, если X<210;
F(x) =1, если X>230.
Определить вероятность отказа прибора из–за непостоянства напряжения сети.
Решение.
Обозначим через A – событие отказа прибора в работе; V – случайная величина напряжения в сети.
P(A)=P(220<V<230)=F(230)-F(220).
F(230)=(x-210)/20=(230-210)/20=1;
F(220)=(220-210)/20=0,5. Откуда P(A)=1-0,5=0,5.
Дата добавления: 2016-04-19; просмотров: 1336;
