Законы распределения случайных величин
Понятие случайной величины
В зависимости от цели того или иного испытания часто имеют дело с величинами, которые могут принимать те или иные значения, причем заранее неизвестно, какие именно. Такие величины называют случайными.
Случайной называется величина, которая в результате опыта может принять одно и только одно возможное значение, заранее неизвестное и зависящее от случайных обстоятельств.
Примеры случайных величин: число вышедших из строя элементов после 1000 часов работы сложного устройства; величина напряжения в сети в данный момент времени; число покупателей в магазине в момент закрытия.
Различают два основных типа случайных величин: дискретные и непрерывные.
К случайным дискретным величинам относят величины, частные значения которых можно пересчитать, т. е. их число конечно.
У случайных непрерывных величин нельзя пересчитать их частные значения, так как их число бесконечно (они непрерывно заполняют определенный интервал).
Случайные величины обозначают прописными буквами X, Y, Z, а их частные значения – строчными буквами x, y, z.
Случайное событие можно рассматривать как частный случай случайной величины.
Например: событие A – попадание пули в мишень, событие 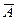 - непопадание пули в мишень. Если случайная величина X принимает частное значение x=1, то появляется событие A, а если случайная величина X принимает частное значение x=0, то появляется событие
- непопадание пули в мишень. Если случайная величина X принимает частное значение x=1, то появляется событие A, а если случайная величина X принимает частное значение x=0, то появляется событие 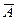 .
.
Законы распределения случайных величин
Всякое соотношение, устанавливающее связь между частным значением случайной величины и вероятностью ее появления, называют законом распределения.
Если случайная величина X принимает частные значения 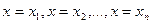 с вероятностью
с вероятностью 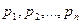 , то закон распределения случайной величины запишется в виде соотношений
, то закон распределения случайной величины запишется в виде соотношений
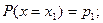
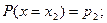
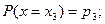
…………….
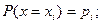
…………….
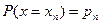 .
.
К основным математическим формам законов распределения случайной величины относят:
ряд распределения,
многоугольник распределения,
функцию распределения,
плотность распределения.
Ряд распределения применяется для случайных дискретных величин и представляет собой таблицу, в первой строке которой указываются частные значения случайной величины, а во второй – вероятности их появления (таблица 1).
Таблица 1
| x | 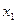
| 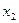
| 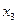
| … | 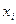
| … | 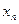
|
| P(X=x) | 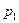
| 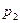
| 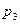
| … | 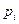
| … | 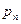
|
Эта таблица позволяет найти ответы на следующие вопросы.
Какие частные значения может принимать случайная величина?
Какие частные значения случайной величины будут появляться чаще, а какие реже?
По этой таблице можно определить вероятность появления случайной величины в заданных пределах 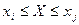 , т.е.
, т.е.
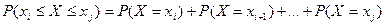 .
.
Многоугольник распределенияпредставляет собой график, на котором по оси абсцисс откладываются частные значения случайной величины, а по оси ординат – вероятности их появления.
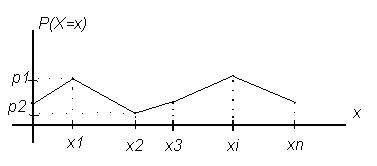
Рисунок 1 Многоугольник распределения
График многоугольника распределения решает те же вопросы, что и ряд распределения.
Ряд и многоугольник распределения не являются универсальными характеристиками случайной величины. Их нельзя построить для случайной непрерывной величины. Поэтому необходима универсальная характеристика, пригодная не только для дискретных, но и для непрерывных величин. Такой характеристикой является функция распределения (интегральная функция) случайной величины, которая обозначается F(x).
Функцией распределения случайной величиныназывают вероятность того, что случайная величина примет частное значение меньшее некоторого фиксированного, т.е.
P(X<x) =F(x).
Геометрически это равенство можно истолковать так: функция распределения F(x) есть вероятность того, что случайная величина X примет значение, которое изображается точкой, лежащей левее точки x.
Так как случайная дискретная величина может принимать значения 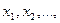 то функция распределения для нее будет
то функция распределения для нее будет
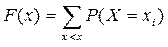 .
.
Дата добавления: 2016-04-19; просмотров: 1255;
