Общие понятия динамического программирования

Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на этапы.

Приведем общую постановку задачи ДП. Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п. В результате управления система (объект управления) S переводится из начального состояния s₀ в состояние 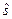. Предположим, что управление можно разбить на n шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное, представляет собой совокупность n пошаговых управлений.

Обозначим через Х_k, управление на k-м шаге (k=1, 2, ..., n). Переменные Х_k, удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми (Х_k может быть числом, точкой в n-мерном пространстве, качественным признаком).

Пусть Х(Х₁, Х₂, ..., Х_n,) — управление, переводящее систему S из состояния s₀ в состояние 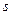. Обозначим через s_k состояние системы после k-го шага управления. Получаем последовательность состояний s₀, s₁, ..., s_k-1,…, s_n= 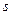, которую изобразим кружками (рис. 7.1).

Рис. 7.1

Показатель эффективности рассматриваемой управляемой операции — целевая функция — зависит от начального состояния и управления:

Z=F(s₀,X) (7.1)

Сделаем несколько предположений.

1. Состояние s_k системы в конце k-го шага зависит только от предшествующего состояния s_k-1 и управления на k-м шаге Х_k, (и не зависит от предшествующих состояний и управлений). Это требование называется “отсутствием последействия”. Сформулированное положение записывается в виде уравнений

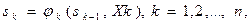
которые называются уравнениями состояний.

2. Целевая функция (7.1) является аддитивной от показателя эффективности каждого шага. Обозначим показатель эффективности k-го шага через 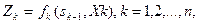Тогда

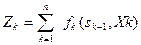(7.2)

Задача пошаговой оптимизации (задача ДП) формулируется так: определить такое допустимое управление Х, переводящее систему S из состояния в s₀ в состояние 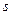, при котором целевая функция (7.2) принимает наибольшее (наименьшее) значение.

Выделим особенности модели ДП:

1. Задача оптимизации интерпретируется как n-шаговый процесс управления.

2. Целевая функция равна сумме целевых функций каждого шага.

3. Выбор управления на k-м шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (нет обратной связи).

4. Состояние s_k после k-го шага управления зависит только от предшествующего состояния s_k-1 и управления Х_k (отсутствие последействия).

5. На каждом шаге управление Х_k, зависит от конечного числа управляющих переменных, а состояние s_k — от конечного числа параметров.