Пример решения задачи
Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: s0 = 5 усл. ед. Размеры вложения в каждое предприятие кратны 1 усл. ед. Средства х, выделенные k-му предприятию (k=1, 2, 3, 4), приносят в конце года прибыль fk(х). Функции fk (х) заданы таблично (табл. 7.1.1). Принято считать, что:
а) прибыль fk(х) не зависит от вложения средств в другие предприятия;
б) прибыль от каждого предприятия выражается в одних условных единицах;
в) суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.
Таблица 7.1.1
| x | f1(x) | f2(x) | f3(x) | f 4(x) |
Решение. Обозначим через хk количество средств, выделенных k-му предприятию. (Нумерацию предприятий 1, 2, 3, 4 сохраняем в процессе решения неизменной.)
Суммарная прибыль равна
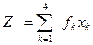 , хk≥0,k=1,2,3,4.
, хk≥0,k=1,2,3,4.
Переменные х удовлетворяют ограничениям:
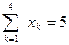 , хk≥0,k=1,2,3,4.
, хk≥0,k=1,2,3,4.
Требуется найти переменные х1, х2, х3, х4, удовлетворяющие системе ограничений и обращающие в максимум функцию.
Особенности модели. Ограничения линейные, но переменные целочисленные, а функции fk (хk) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств s0=5 можно рассматривать как 4-шаговый, номер шага совпадет с номером предприятия; выбор переменных х1, х2, х3, х4 — управление соответственно на I, II, III, IV шагах. 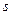 - конечное состояние процесса распределения — равно нулю, так как все средства должны быть вложены в производство,
- конечное состояние процесса распределения — равно нулю, так как все средства должны быть вложены в производство, 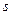 =0. Схема распределения показана на рис. 7.1.1.
=0. Схема распределения показана на рис. 7.1.1.
Уравнения состояний в данной задаче имеют вид:
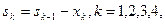
где sk - параметр состояния - количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися
4 - k предприятиями.
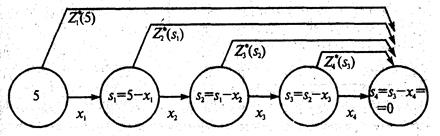
Рис. 7.1.1
Введем в рассмотрение функцию 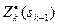 - условную оптимальную прибыль, полученную от k-го,..., 4-го предприятий, если между ними распределялись оптимальным образом средства sk-1(0≤ sk-1≤5). Допустимые управления на k-м шаге удовлетворяют условию: 0≤xk≤ sk-1 (либо k-му предприятию ничего не выделяем, хk=0, либо не больше того, что имеем к к-му шагу, xk≤ sk-1 .
- условную оптимальную прибыль, полученную от k-го,..., 4-го предприятий, если между ними распределялись оптимальным образом средства sk-1(0≤ sk-1≤5). Допустимые управления на k-м шаге удовлетворяют условию: 0≤xk≤ sk-1 (либо k-му предприятию ничего не выделяем, хk=0, либо не больше того, что имеем к к-му шагу, xk≤ sk-1 .
Уравнения имеют вид:
k=4,  (a)
(a)
 (б)
(б)
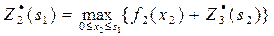 (в)
(в)
 (г)
(г)
Последовательно решаем записанные уравнения, проводя условную оптимизацию каждого шага.
IV ш а г. В таблице 7.1.1 f 4(x) прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4-е предприятие. При этом для возможных значений s3=0, 1, ..., 5 получим:
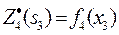 и
и 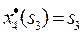
III ш а г. Делаем все предположения относительно остатка средств s2 к III шагу (т.е. после выбора х1 и х2). s2 может принимать значения 0, 1, 2, 3, 4, 5. В зависимости от этого выбираем 0≤ х3≤s2, находим s3=s2-x3 и сравниваем для разных х3 при фиксированном s2 значения суммы 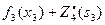 . Для каждого s2 наибольшее из этих значений есть
. Для каждого s2 наибольшее из этих значений есть 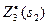 - условная оптимальная прибыль, полученная при оптимальном распределении средств s2 между 3-м и 4-м предприятиями.
- условная оптимальная прибыль, полученная при оптимальном распределении средств s2 между 3-м и 4-м предприятиями.
II ш а г. Условная оптимизация, согласно уравнению (в), проведена в таблице 7.1.2. при k=2.
I ш а г. Условная оптимизация (уравнение (г) проведена в табл. 7.1.2 при k=1 для s0=5. Поясним решение подробно: если х=0, то s1=5, прибыль, полученная от четырех предприятий при условии, что s1=5 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна  . Если х1=1, то s2=4. Суммарная прибыль при условии, что s2=4 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна
. Если х1=1, то s2=4. Суммарная прибыль при условии, что s2=4 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна 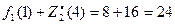 . Аналогично при х1=2, s2= 3 и
. Аналогично при х1=2, s2= 3 и  ;
;
при х1=3, s2= 2 и 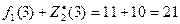 ;
;
при х1=4, s2= 1 и 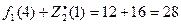 ;
;
при х1=5, s2= 0 и 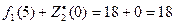 .
.
Сравнивая числа, получим 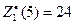 усл. ед. =Zmax при
усл. ед. =Zmax при 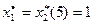 .
.
Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию — 2 усл. ед.; 3-му предприятию — 1 усл. ед.; 4-му предприятию — 1 усл.ед.
Таблица 7.1.2
| S k-1 | xk | sk | K=3 | K=2 | K=1 | ||||||

| 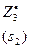
| 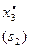
| 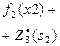
| 
| 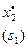
| 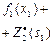
| 
| 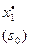
| |||
| 0+1=1 | 0+4=4 | 0+6=6 | |||||||||
| 3+1=3 | 6+0=6 | 8+0=8 | |||||||||
| 0+6=6 | 0+7=7 | 0+10=10 | |||||||||
| 3+4=4 | 6+4=10 | 8+6=14 | |||||||||
| 4+0=4 | 9+0=9 | 10+0=10 | |||||||||
| 0+8=8 | 0+9=9 | 0+13=13 | |||||||||
| 3+6=9 | 6+7=13 | 8+10=18 | |||||||||
| 4+4=8 | 9+4=13 | 10+6=16 |
Сетевая модель
Сетевая модель – план выполнения некоторого комплекса взаимосвязанных работ, заданного в специфической форме сети, графическое изображение которого называется сетевым графиком.
Событие – момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта.
Порядок построения сетевого графика.
1. В сетевой модели не должно быть “тупиковых” событий, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события.
2. В сетевом графике не должно быть событий (кроме исходного), которым не предшествует хотя бы одна работа.
3. В сети не должно быть замкнутых контуров и петель, т. е путей, соединяющих некоторые события с ними же самими.
4. Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой.
5. В сети рекомендуется иметь одно исходное и одно завершающее событие.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.
Критический путь – наиболее продолжительный полный путь в сетевом графике.
Временные параметры сетевых графиков
| Элемент сети, характеризуемый параметром | Наименование параметра | Условное обозначение параметра |
| Событие i | Ранний срок свершения события Поздний срок свершения события Резерв времени события | tp(i) tn(i) R(i) |
| Работа (i,j) | Продолжительность работы Ранний срок начала работы Ранний срок окончания работы Поздний срок начала работы Поздний срок окончания работы Полный резерв времени работы Частный резерв времени работы первого вида Частный резерв времени работы второго вида иди свободный резерв времени работы Независимый резерв времени работы | t(i,j) tрн(i,j) tро(i,j) tпн(i,j) tпо(i,j) Rп(i,j) R1(i,j) Rс(i,j) Rн(i,j) |
| Путь L | Продолжительность пути Продолжительность критического пути Резерв времени пути | t(L) tкр R(L) |
Оптимизация сетевого графика – процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения.
Частная оптимизация – минимизация времени выполнения комплекса работ при заданной стоимости, минимизация стоимости комплекса работ при заданном времени выполнения проекта.
Комплексная оптимизация – нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.
Дата добавления: 2016-04-19; просмотров: 1424;
