Пример решения задачи. Геометрически решить следующую задачу ВП: найти минимум функции Z = 2 + (х1 — 1)2 + (х2 -1)2 при ограничениях:

Геометрически решить следующую задачу ВП: найти минимум функции Z = 2 + (х₁ — 1)² + (х₂ -1)² при ограничениях:

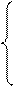
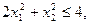
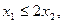
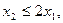
х₁³0, х₂³0

Решение. Строим область допустимых решений данной задачи:

а) х₁² + х₂² = 4 — окружность с центром в начале координат и радиусом R= 2. (рис. 6.1). Область решений неравенства х₁² + х₂² ≤4 состоит из точек, лежащих внутри этой окружности и на ней самой;

б) х₁ = 2х₂ — прямая, которую можно построить, например, по точкам (0; 0) и (2; 1). Область решений неравенства х₁ ≤ 2х₂ — полуплоскость, лежащая над этой прямой, включая и саму прямую;

в) х₂ = 2х₁ — прямая, которая строится, например, по точкам (0; 0) и (1; 2). Область решений неравенства х₂ ≤ 2х₁ - полуплоскость, лежащая под этой прямой, включая и саму прямую. Таким образом, с учетом условий неотрицательности переменных, областью допустимых решений данной задачи является замкнутый сектор ОАВ (рис. 6.1.1).

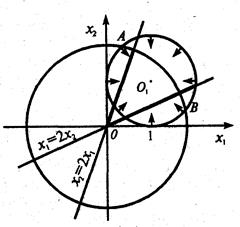
Рис. 6.1.1

Теперь построим линию уровня функции Z и определим направление убывания Z. Все линии уровня имеют Z = С, т.е. (х₁ -1)²+(х₂ - 1)² = C - 2. При С= 3 получаем линию, уровня (х₁ - 1)²+(х₂ - 1)² = 1 - это окружность с центром в точке О₁(1; 1) и радиусом R = 1. Ясно, что в любой точке этой линии уровня при перемещении от центра окружности О₁ функция Z возрастает, а при перемещении к центру — убывает. Таким образом, минимум Z достигается в точке (1; 1), Z_min= 2 (нетрудно убедиться, что точка (1; 1) является стационарной точкой функции Z).