Пример решения задачи. Оптимизировать сетевой график, изображенный на рис
Оптимизировать сетевой график, изображенный на рис. 8.1.1., на котором указаны максимально возможные продолжительности работ (в сутках). Необходимые для оптимизации исходные данные представлены в таблице.
Таблица 8.1.1
| № п/п | Работа (i,j) | Продолжительность работы, сутки | Коэффициент затрат на ускорение работы h(i,j) | Стоимость работы, усл. руб. С=(i,j) при t(i,j)= b (i,j) | |
| мини- мальная а(i,j) | макси- мальная b (i,j) | ||||
| (0,1) | |||||
| (0,2) | |||||
| (1,2) | |||||
| (1,3) | |||||
| (2,7) | |||||
| (3,4) | |||||
| (3,5) | |||||
| (4,6) | |||||
| (5,6) | |||||
| (6,7) | |||||
| (7,8) | |||||
| Итого |
Решение. Исходный для оптимизации план (см. рис.8.1.1) имеет максимальную продолжительность работ t(i,j)= b (i,j) и соответственно минимальную стоимость С=З00 (усл. руб.). Найдем все полные пути сетевого графика.
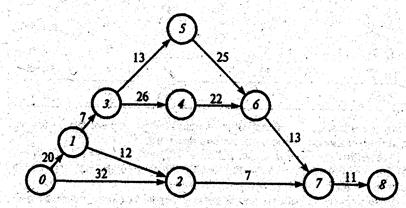
Рис. 8.1.1
Их четыре:
L1 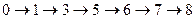 продолжительностью t(L1)=89 (суток);
продолжительностью t(L1)=89 (суток);
L2 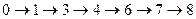 продолжительностъю tкр= t(L2)=99 (суток);
продолжительностъю tкр= t(L2)=99 (суток);
L3 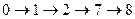 продолжительностью t(L3)=50(сугок);
продолжительностью t(L3)=50(сугок);
L4 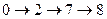 продолжительностью t(L4)=50 (сугок).
продолжительностью t(L4)=50 (сугок).
Для удобства дальнейших расчетов представим эти пути графически в виде цепочек работ (рис. 8.1.2), в которых цифры над стрелками показывают коэффициенты затрат на ускорение работ h(i,j), а под стрелками — максимально возможные величины уменьшения продолжительности работ Dt(i,j) = b (i,j)- а(i,j).
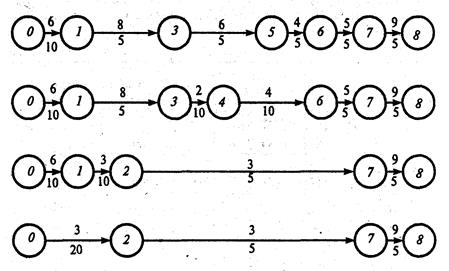
Рис. 8.1.2
I ш а г. Уменьшить продолжительность выполнения комплекса можно, как известно, только за счет сокращения продолжительности работ критического пути tкр=t(L2). Из работ критического пути L2 наименьший коэффициент затрат на ускорение h(i,j) имеет работа (3,4):
hmin(i,j)= min{h (0, 1); h (1, .3); h (3, 4); h (4, б); h (б, 7);
h (7, 8)}= min{6; 8; 2; 4; 5; 9}=2, т.е. hmin(i,j)= h (3, 4)=2. Продолжительность работы t(3,4) можно сокращать не более чем на 10 суток. При этом изменится длина только критического пути (с 99 до 89 суток) — L2 единственного из четырех путей, проходящего через работу (3,4). А стоимость проекта за счет ускорения работы (3,4) возрастет до 320 (усл. руб.). Итак, на 1 шаге:
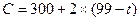 , где 89≤t≤99;
, где 89≤t≤99;
новые длины путей равны t(L1)= t(L2)=89; t(L3)= t(L4)=50.
II ш а г. Теперь мы имеем два критических пути L1 и L2 и сократить срок выполнения проекта можно за счет одновременного сокращения их продолжительности. Сократить одновременно t(L1) и t(L2) можно, уменьшив продолжительность работ, лежащих на этих путях: либо t(0, 1), либо t(6,7), либо t(7, 6). Останавливаемся на t(6, 7), поскольку при этом обеспечивается минимум затрат на ускорение работы: hmin(i,j)=min{h(0,1);h(1,3); h(6,7); h(7,8)}=min{6; 8; 5; 9}=5, т.е.
hmin(i,j)=h (6, 7)=5.
Продолжительность работы t(6,7), можно уменьшить не более на 5 суток. На эту величину уменьшатся длины критических путей t(L1) и t(L2), а следовательно, и срок выполнения проекта t= t(L1) и t= t(L2). При этом стоимость проекта увеличится с 320 до 345 (усл. руб.). Итак, на II шаге:
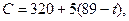 где 84≤t≤89;
где 84≤t≤89;
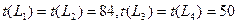
Продолжая аналогичным образом сокращать продолжительность работ, получим
III ш а г. hmin(i,j)= min {h(0, 1); h(1, 3); h(7, 8)} = min (6; 8; 9}=6, т.е. hmin(i,j)=h(0,1)=6. Сокращая продолжительностъ работы t(0, 1) до 10 суток, найдем
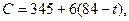 где 74≤t≤84
где 74≤t≤84
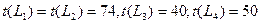
IV ш а г. hmin(i,j)= min {h(1, 3); h(7,6)} = min {8; 9} = 8, т.е.
hmin(i,j)= h(1, 3)= 8. Сокращая продолжительность работы t(1, З) до 5 суток, найдем
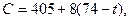 где 69≤t≤74
где 69≤t≤74
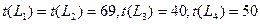
V ш а г. Сокращая продолжительность работы t (7, 8) до 5 суток, найдем (учитывая, что h (7, 8)=9)
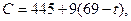 где 64≤t≤69
где 64≤t≤69
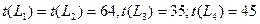
VI ш а г. Теперь несокращенными остались продолжительности трех критических работ: t(3, 5) и t(5, 6) критического пути L1, каждую из которых можно сократить до 5 суток, и t(4, 6) критического пути L2, которую можно сократить до 10 суток. Сокращение какой-либо одной из названных величин не приведет к сокращению продолжительности выполнения проекта, ибо при этом сократится лишь один из двух путей, а длина несокращенного пути, который станет единственным критическим путем, не изменится. Поэтому последовательно сокращая t(4, 6) и t(5, 6) до 5 суток (с учетом времени сокращения продолжительности работ), найдем (теперь коэффициент затрат на ускорение работ равен
h(4, 6)+h(5, 6)= 4+4= 8):
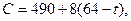 где 59≤t≤64;
где 59≤t≤64;
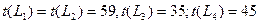
VII ш а г. Продолжительность работы t(4, 6) можно сократить еще до 5 суток и на тот же срок можно сократить t (3, 5) (иначе срок выполнения проекта не изменится). Полагая, что h (4, 6)+h (3, 5)=4+6=10, найдем
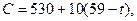 где 54≤t≤59
где 54≤t≤59
График оптимальной зависимости стоимости проекта С(t) от продолжительности его выполнения показан на рис. 8.1.3. С помощью этого графика можно, с одной стороны, оценить минимальную стоимость проекта при любом возможном сроке его выполнения, а с другой стороны — найти предельную продолжительность выполнения проекта при заданной его стоимости. Например, при продолжительности проекта t=79 (суток) минимальная стоимость выполнения рассматриваемого комплекса составит 375 (усл. руб.), а при стоимости выполнения комплекса, например, 540 (усл. руб.) предельная продолжительность проекта составит 55 (суток). С помощью функции С(t) можно оценить дополнительные затраты, связанные с сокращением сроков завершения комплекса. Так, сокращение продолжительности проекта с 79 до 55 суток потребует дополнительных затрат 540-375=165 (усл. руб.).
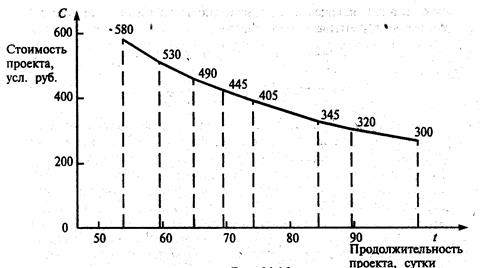
Рис. 8.1.3
Дата добавления: 2016-04-19; просмотров: 1408;
