Пример транспортной задачи
Построить экономико-математическую модель следующей задачи. Имеются три поставщика и четыре потребителя. Мощность поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары “поставщик — потребитель” сведены в таблицу поставок (табл. 4.1.1).
Таблица 4.1.1
| Поставщики | Мощность поставщиков | Потребители и их спрос | |||
| х11 | х12 | х13 | х14 | ||
| х21 | х22 | х23 | х24 | ||
| х31 | х32 | х33 | х34 |
В левом верхнем углу произвольной (ij-клетки (i - номер строки,
j - номер столбца) стоит так называемый коэффициент затрат — затраты на перевозку единицы груза от i-го поставщика к j-му потребителю, например, в левом верхнем углу клетки (1,4) стоит число 3, следовательно, перевозка единицы груза от 1-го поставщика к 4-му потребителю обойдется в 3 условных денежных единицы и т. д.
Задача ставится следующим образом: найти объемы перевозок для каждой пары «поставщик — потребитель» так, чтобы:
1) мощности всех поставщиков были реализованы;
2) спросы всех потребителей были удовлетворены;
3) суммарные затраты на перевозку были бы минимальны.
Решение. Построим экономико-математическую модель данной задачи, Искомый объем перевозки от i-го поставщика к j-му потребителю обозначим черёз xij и назовём поставкой клетки (i,j). Например, х12 — искомый объем перевозки от 1- го поставщика ко 2-му потребителю или поставка клетки (1,2) и т. д. Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения неизвестных х. Так, например, объем груза, забираемого от 1 -го поставщика, должен быть равен мощности этого поставщика — 60 единицам, т.е.
х11+ х12 + х13 + х14 = 60 (уравнение баланса по первой строке). Таким образом, чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, т. е.
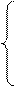
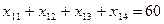 ,
,
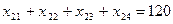 , (4.1.1)
, (4.1.1)
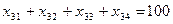 .
.
Аналогично, чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляем для каждого столбика таблицы поставок:
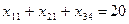 ,
,
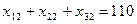 , (4.1.2)
, (4.1.2)
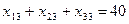 ,
,
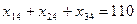 .
.
Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует дополнительно предположить, что
хij≥0 (i= 1, 2, 3; j= 1, 2, 3, 4).
Суммарные затраты Р на перевозку выражаются через коэффициенты затрат и поставки следующим образом;
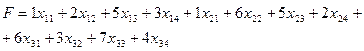 (4.1.3)
(4.1.3)
Найдем первоначальное базисное распределение поставок для транспортной задачи методом «северо-западного угла».
Решение. Дадим переменной х11 максимально возможное значение или, иными словами, максимально возможную поставку в клетку (1,1) — “северо-западный” угол таблицы поставок: х11= min {60, 20) = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпадет из последующего рассмотрения (заполненные клетки будем перечеркивать сплошной линией (см. табл. 4.1.2) клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией. В таблице поставок найдем новый “северо-западный” угол — клетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1-й поставщик уже отдал 20 единиц груза и у него осталось только 40 = 60—20 единиц груза, получаем, что х12 = min {40, 110} = 40. После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной линией клетку (1,2) и пунктирной линией оставшиеся свободные клетки первой строки). В оставшейся таблице снова находим “северо-западный угол” и т. д. В результате получаем следующее исходное распределение поставок (см. табл.4.1.2).
Таблица 4.1.2
Решение методом наименьших затрат.
Решение. Находим в таблице поставок (см. табл.4.1.1) клетки с наименьшим коэффициентом затрат. Таких клеток две – (1,1) и (2,1) с коэффициентами затрат, равными 1. Сравним максимально возможные поставки для этих клеток: для клетки (1,1) х11 = min {60, 20}= 20, для клетки (2,1) x21= min {120, 20}=20.
Так как они совпадают, то максимально возможную поставку даем в любую из них. Например, даем поставку, равную 20 единицам, в клетку (2,1). В результате спрос первого потребителя удовлетворен и первый столбец таблицы поставок выпадает из последующего рассмотрения (табл. 4.1.3).
Таблица 4.1.3
В оставшейся таблице наименьшим коэффициентом затрат обладают две клетки: с12 = с24= 2. Сравним максимально возможные поставки для этих клеток: для клетки (1,2) х12 = min {60, 110} = 60; для клетки (2,4) х24 = min {120-20, 110} = 100. Даем поставку в клетку (2,4), для которой максимально возможная поставка оказалась больше: х24 =100. При этом из рассмотрения выпадает вторая строка таблицы поставок (табл. 4.1.4).
Таблица 4.1.4
Аналогично, продолжая заполнение таблицы поставок шаг за шагом, получаем х12 = min{60, 110} = 60,x32 = min {100, 110—60} = 50,
х34 =min {100—50, 110—100}=10, x33 = min {100-60, 40} = 40, табл. 4.1.5
Таблица 4.1.5
Дата добавления: 2016-04-19; просмотров: 1100;
