Уравнение колебаний
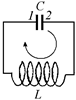 Рис. 15.4
Рис. 15.4
|
Попробуем выяснить, как зависят от времени заряд на обкладке конденсатора и сила тока в колебательном контуре (рис. 15.4). Но прежде, чем мы приступим к вычислениям, отметим следующее:
1) ток в процессе колебаний течет то в одном, то в другом направлении. Чтобы величина силы тока в данный момент времени была определена однозначно, необходимо задать направление обхода контура. Тогда ток, текущий вдоль направления обхода, считаем положительным, а против – отрицательным;
2) заряды на пластинах конденсатора всегда равны по величине и противоположны по знаку, поэтому надо договориться, заряд какой пластины (1 или 2) в данный момент мы рассматриваем;
3) напряжение между пластинами конденсатора – это разность между потенциалами пластин. Эта величина, как и сила тока, меняет знак в процессе колебаний. Чтобы величина была однозначно определена в данный момент времени, договоримся, что мы считаем напряжением U = j1 – j2 или U = j2 – j1, где j1 и j2 – потенциалы пластин 1 и 2 соответственно.
С учетом данных замечаний приступим к установлению зависимости от времени заряда q(t), тока i(t) и напряжения и(t):
1) зададим направление обхода контура по часовой стрелке (см. рис. 15.4);
2) назовем «первой» ту пластинку конденсатора, которая встретилась первой после катушки при следовании по направлению обхода контура, а «второй» – смежную с ней пластину. Зарядом конденсатора будем называть заряд первой пластины;
3) под напряжением будем понимать величину U = j1 – j2. Если q1 > 0, а q2 = –q1 < 0, то  , а если q1 < 0, то
, а если q1 < 0, то 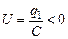 .
.
Теперь приступим к расчетам.
Пусть в колебательном контуре емкость конденсатора равна С, а индуктивность катушки – L. Пусть в некоторый момент времени t заряд пластины 1 равен q(t), а сила тока i(t). Тогда за малое время Dt заряд пластины 1 изменится на величину Dq = i(t)Dt.
Величина Dq может быть положительной, если ток в данный момент времени t течет по направлению обхода, тогда i(t) > 0. Но величина Dq может быть и отрицательной, если ток в данный момент времени t течет против направления обхода, тогда i(t) < 0. В любом случае 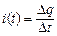 . При Dt ® 0 это означает, что
. При Dt ® 0 это означает, что
i(t) = q¢(t). (15.3)
Если в произвольный момент времени t заряд пластины 1 равен q(t), а сила тока равна i(t) (знаки для q(t) и i(t) значения не имеют), то энергия системы в этот момент равна
 +
+ =
= . (15.4)
. (15.4)
Продифференцируем выражение (15.4) по времени:
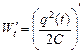 +
+ =
=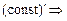
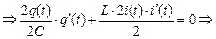
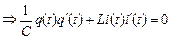 .
.
Подставим в последнее равенство значение i(t) = q¢(t) из (15.3) и получим:
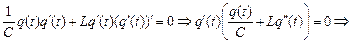

Введем обозначение 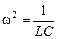 , тогда последнее уравнение примет вид
, тогда последнее уравнение примет вид

Это – хорошо знакомое нам дифференциальное уравнение, которое уже неоднократно встречалось при изучении гармонических колебаний (§ 1).
При начальном условии q(t) = qm его решение имеет вид:
q(t) = qmcos(wt), (15.5)
С учетом того, что напряжение на конденсаторе 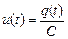 , можем записать:
, можем записать:
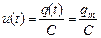 cos(wt), (15.6)
cos(wt), (15.6)
где 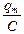 = ит – амплитуда напряжения. А с учетом формулы (15.3) получим выражение для тока:
= ит – амплитуда напряжения. А с учетом формулы (15.3) получим выражение для тока:
i(t) = q¢(t) = (qmcos(wt))¢ = qm(–sinwt)w = –qmwsinwt.
Запомним:
i(t) = –qmwsinwt. (15.7)
Здесь qmw = Im – амплитудное значение силы тока.
Графики зависимости заряда и тока от времени имеют вид двух синусоид, сдвинутых друг относительно друга на p/2. При этом заряд «опережает» ток (рис. 15.5).
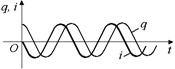 Рис. 15.5
Рис. 15.5
|
Циклическая частота колебаний равна
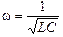 . (15.8)
. (15.8)
Частота колебаний
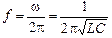 . (15.9)[4]
. (15.9)[4]
Период колебаний
 . (15.10)
. (15.10)
СТОП! Решите самостоятельно: В1–В3, С1–С2.
Задача 15.1. В каких пределах должна изменяться индуктивность катушки колебательного контура, чтобы в контуре происходили колебания с частотой от f1 = 400 Гц до f2 = 500 Гц. Емкость конденсатора С = 10 мкФ.
| f1 = 400 Гц f2 = 500 Гц С = 10 мкФ | Решение. Воспользуемся формулой (15.9):
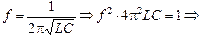 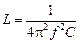 ,
отсюда ,
отсюда
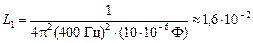 Гн; Гн;
|
| L1 = ? L2 = ? | |
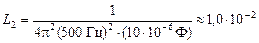 Гн.
Гн.
Ответ: индуктивность должна изменяться от 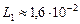 Гн до
Гн до 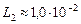 Гн.
Гн.
СТОП! Решите самостоятельно: А1–А4.
Задача 15.2. Период электрических колебаний в контуре 1,0×10–5 с. При подключении параллельно конденсатору контура дополнительного конденсатора электроемкостью 3,0×10–8 Ф период колебаний увеличился в два раза. Определите индуктивность катушки и начальную электроемкость конденсатора колебательного контура.
| Т1 = 1,0×10–5 с С2 = 3,0×10–8 Ф Т2/Т1 = 2 | Решение. Вспомним, что при параллельном соединении емкости конденсаторов складываются, и применим формулу Томсона для обоих случаев:
Т1 =  , (1)
2Т1 = , (1)
2Т1 = 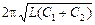 , (2) , (2)
|
| L = ? C1 = ? | |
Разделим (2) на (1) и получим
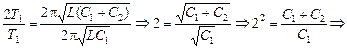

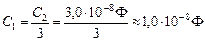 .
.
Выразим индуктивность L из (1):
Т1 = 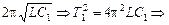
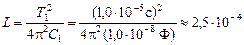 Гн.
Гн.
Ответ: 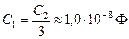 ,
, 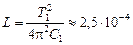 Гн.
Гн.
СТОП! Решите самостоятельно: В4–В6, С3–С5.
Задача 15.3. Колебательный контур состоит из катушки индуктивностью L = 0,20 Гн и конденсатора емкостью С = 1,0×10–5 Ф. Конденсатор зарядили до напряжения U = 2,0 В, и он начал разряжаться. Каким будет ток в момент, когда энергия контура окажется поровну распределенной между электрическим и магнитным полем?
| L = 0,20 Гн С = 1,0×10–5 Ф U = 2,0 В Wм = Wэ | Решение. Энергия контура равна 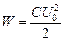 . В тот момент, когда энергии электрического и магнитного полей равны, на долю энергии магнитного поля приходится ровно половина полной энергии контура, поэтому . В тот момент, когда энергии электрического и магнитного полей равны, на долю энергии магнитного поля приходится ровно половина полной энергии контура, поэтому
|
| i = ? | |

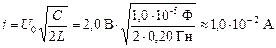 .
.
Ответ: 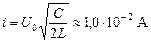 .
.
СТОП! Решите самостоятельно: А5–А7, В7–В9.
Задача 15.4.Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t по закону q = =10-6cosl04pt. Записать закон зависимости силы тока от времени i(t). Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока. Все величины считать точными и заданными в единицах СИ.
| q = 10-6cosl04pt | Решение. Воспользуемся формулой (15.3) i(t) = = q¢(t): i(t) = (10-6cosl04pt)¢ = 10-6 (–sinl04pt)×104p = = –10–2psin104pt. |
| i(t) = ? T = ? f = ? qm = ? im = ? | |
Учитывая, что q = qmcoswt, а i = –imsinwt, легко находим значения заряда и тока:
qm = 10–6 Кл; im = 10–2p А.
Находим амплитуду колебаний заряда и амплитуду колебаний силы тока:
w = 104p Þ  Гц;
Гц;
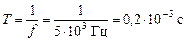 .
.
Ответ: i(t) = –10–2psin104pt; qm = 10–6 Кл;
im = 10–2p А; w = 5×103 Гц; 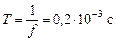 .
.
СТОП! Решите самостоятельно: В10–В12, С6.
Дата добавления: 2016-04-11; просмотров: 3325;
