С законом всемирного тяготения вы познакомились в 7 классе. Напомним его формулировку.
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Две точечные массы т1 и т2, расположенные на расстоянии R друг от друга, притягиваются с силой F, равной
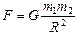 , (17.1)
, (17.1)
где G = 6,67.10–11 (Н×м2)/кг2 – гравитационная постоянная.
Под точечными массами мы понимаем тела, размерами которых можно пренебречь по сравнению с расстоянием между ними.
Если взаимодействуют два однородных шара, то даже если расстояние между ними сравнимо с их размерами, формулу (17.1) применять можно, только под величиной R следует понимать расстояние между центрами шаров.
Если тело находится на поверхности планеты (Земли, например), то сила тяготения Fт, которую в этом случае называют силой тяжести, также может быть вычислена по формуле (17.1), где в качестве R следует взять радиус планеты.
Автор: Как Вы считаете во сколько раз увеличится (и увеличится ли?) сила тяжести, действующая на тело массой т, если радиус Земли увеличить в 2 раза? Тело находится на поверхности Земли.
Читатель: С одной стороны, чем больше радиус планеты, тем больше ее масса, а с другой – тем дальше тело, находящееся на поверхности планеты, удалено от ее центра. Даже не знаю…
Автор: Вспомним, что масса равна произведению плотности на объем: т = rV, а объем шара радиусом R равен V = 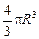 . Тогда сила, с которой планета массой М притягивает тело массой т, равна
. Тогда сила, с которой планета массой М притягивает тело массой т, равна
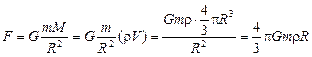 .
.
Итак, мы получили еще одну формулу для вычисления силы тяжести на поверхности планеты плотностью r и радиусом R:
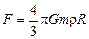 . (17.2)
. (17.2)
Получается, что при данной плотности сила тяжести прямо пропорциональна радиусу планеты, а значит, увеличив радиус Земли в 2 раза, мы и силу тяжести увеличим в 2 раза.
Как вычислить g?
Вы знаете, что вблизи поверхности Земли все тела падают с одинаковым ускорением g = 9,8 м/с2, а сила тяжести, действующая на тело массой т,равна:
Fт = mg. (17.3)
С другой стороны, согласно формуле (17.1) сила, с которой Земля массой М притягивает тело массой т, равна:
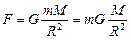 . (17.4)
. (17.4)
Приравняв правые части формул (17.3) и (17.4), получим:
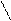
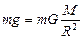 Þ
Þ
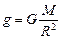 . (17.5)
. (17.5)
Заметим, что по формуле (17.5) можно вычислить ускорение свободного падения не только для Земли, но и для любой другой шарообразной планеты.
Если в формулу (17.5) подставить значение
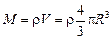 ,
,
получим еще одну формулу для вычисления g:
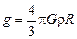 . (17.6)
. (17.6)
Дата добавления: 2016-04-11; просмотров: 973;
