Что такое сила инерции?
Пусть на некоторое тело массы т, движущееся в неинерциальной с.о. х¢0¢у¢ с ускорением 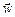 ¢ действуют силы:
¢ действуют силы: 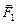 ,
, 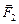 , …,
, …, 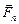 и пусть с.о. х¢0¢у¢ движется относительно инерциальной с.о. х0у с ускорением
и пусть с.о. х¢0¢у¢ движется относительно инерциальной с.о. х0у с ускорением 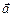 . Тогда согласно формуле (18.1) в и.с.о. х0у тело движется с ускорением
. Тогда согласно формуле (18.1) в и.с.о. х0у тело движется с ускорением 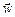 =
= 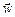 ¢ +
¢ + 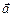 , и можно для этой и.с.о. записать второй закон Ньютона в виде
, и можно для этой и.с.о. записать второй закон Ньютона в виде
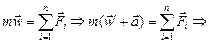
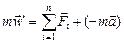 .
.
Введем обозначение 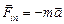 , тогда последнее равенство примет вид
, тогда последнее равенство примет вид
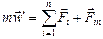 . (18.2)
. (18.2)
А величину 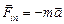 назовем силой инерции.
назовем силой инерции.
Читатель: Простите, но какая же это сила? Ведь от того, что мы сделали чисто математическое преобразование, перенеся член 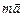 из левой части равенства в правую, никаких реальных сил, конечно же, появиться не может! Зачем же сбивать меня с толку?
из левой части равенства в правую, никаких реальных сил, конечно же, появиться не может! Зачем же сбивать меня с толку?
Автор: Вы правы, слов нет. Конечно же, наше действие по переносу члена ( 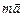 ) из одной части равенства в другую, а затем введение нового термина «сила инерции» носит чисто умственный характер, но все же наша затея имеет смысл.
) из одной части равенства в другую, а затем введение нового термина «сила инерции» носит чисто умственный характер, но все же наша затея имеет смысл.
Как мы с Вами знаем, в н.с.о. второй закон Ньютона не выполняется. А если мы посмотрим на равенство (18.2), то получится, что… выполняется! Если только ко всем реальным силам, действующим на тело, добавить некую умственную силу – силу инерции, равную произведению массы тела на ускорение н.с.о., взятому со знаком «минус». И заметьте, в жизни мы реально не раз ощущаем эту самую силу инерции!
Читатель: Как мы можем ощущать то, чего нет?
Автор: Например, в момент резкого торможения автомобиля, в котором Вы едете. Ведь неслучайно шоферу и пассажиру на переднем сидении настоятельно рекомендуют пристегнуться ремнями! Зачем? Да затем, что при аварийном торможении их резко «бросает» вперед и, если бы не ремни, можно весьма основательно «приложиться» к лобовому стеклу. Кто же толкает пассажира вперед? Так сила инерции и толкает! При торможении ускорение автомобиля направлено назад (рис. 18.3,а), значит в н.с.о. «автомобиль» на пассажира действует сила инерции 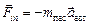 , направленная вперед. Причем она тем больше, чем больше ускорение автомобиля.
, направленная вперед. Причем она тем больше, чем больше ускорение автомобиля.
Читатель: Но ведь этот же эффект можно объяснить без силы инерции: просто пассажир, чтобы приобрести ускорение 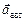 , направленное назад, должен испытать действие силы, направленной назад. Этой силой и является сила упругости ремней безопасности или (если их нет) лобового стекла:
, направленное назад, должен испытать действие силы, направленной назад. Этой силой и является сила упругости ремней безопасности или (если их нет) лобового стекла: 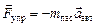 (рис. 18.3,б).
(рис. 18.3,б).
а) 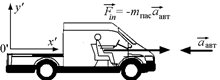 б)
б) 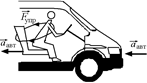
Рис. 18.3
Автор: Можно, конечно, и так. Но при решении ряда задач, связанных с движением тел в н.с.о., понятие «сила инерции» очень удобно. Давайте в этом убедимся.
Задача 18.1. Шарик массы т подвешен на нити, закрепленной на стержне, установленном на тележке, которая движется горизонтально с ускорением а (рис. 18.4,а). Определить силу натяжения нити.
| т а | а) 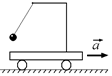 б) б) 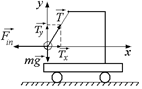
|
| Т = ? | |
| Рис. 18.4 |
Решение. Рассмотрим положение шарика в н.с.о. х0у, связанной с тележкой (рис. 18.4,б). На шарик действуют три силы: 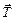 ,
, 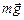 и
и 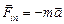 , тогда второй закон Ньютона имеет вид
, тогда второй закон Ньютона имеет вид
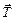 +
+ 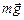 +
+ 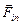 =
= 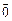 .
.
«Спроецируем» это уравнение на оси х и у:
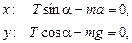
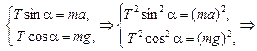
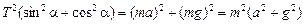 Þ
Þ
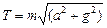 .
.
Ответ: 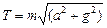
СТОП! Решите самостоятельно: А1–А5, А7, В3.
Задача 18.2. С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок А (рис. 18.5,а), чтобы тела 1 и 2 не двигались относительно него? Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен k. Массы блока и нити пренебрежимо малы, трения в блоке нет.
| т1 = т2 = т k |
а) 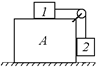 б)
Рис. 18.5 б)
Рис. 18.5
| 
|
| amin = ? | ||
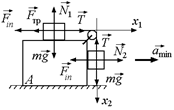
Решение. Перейдем в н.с.о., связанную с бруском А. Тогда на тела 1 и 2 в дополнение ко всем «обычным» силам будет действовать сила инерции 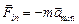 (рис. 18.5,б). Поскольку в н.с.о. оба тела покоятся, а
(рис. 18.5,б). Поскольку в н.с.о. оба тела покоятся, а 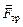 по условию задачи принимает свое максимально возможное значение Fтр = kN1 = kmg, запишем второй закон Ньютона в проекциях на оси х1 и х2:
по условию задачи принимает свое максимально возможное значение Fтр = kN1 = kmg, запишем второй закон Ньютона в проекциях на оси х1 и х2:
х1: T – kmg – mamin = 0,
x2: mg – T = 0.
Сложив эти уравнения, получим
mg – kmg – mamin = 0 Þ amin = g(1 – k).
Ответ: amin = g(1 – k).
СТОП! Решите самостоятельно: А6, В4, В5, С1.
Задача 18.3. Призме 1, на которой находится брусок 2 массы т, сообщили влево горизонтальное ускорение а (рис. 18.6,а). При каком максимальном значении этого ускорения брусок будет оставаться еще неподвижным относительно призмы, если коэффициент трения между ними k < ctga?
а) 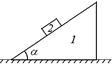
| б) 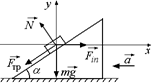
| |
| т а k < ctga | ||
| аmax = ? | ||
Рис. 18.6
Решение. Перейдем в н.с.о. «призма 1», тогда на брусок 2 действуют силы: 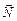 ,
, 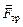 ,
, 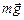 и
и 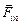 (рис. 18.6,б). При этом, поскольку брусок неподвижен,
(рис. 18.6,б). При этом, поскольку брусок неподвижен, 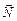 +
+ 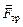 +
+ 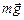 +
+ 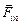 =
= 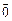 , где
, где 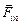 = –
= – 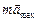 , а
, а 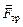 достигает своего максимального значения Fтр = kN. По второму закону Ньютона в проекциях на оси х и у получим:
достигает своего максимального значения Fтр = kN. По второму закону Ньютона в проекциях на оси х и у получим:
х: –Nsina – kNcosa + mamax = 0, (1)
y: Ncosa – kNsina – mg = 0. (2)
Из (2) находим 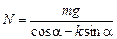 , подставляем это значение в (1) и после преобразований получаем
, подставляем это значение в (1) и после преобразований получаем
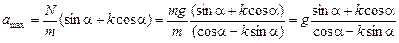 .
.
Если cosa – ksina > 0, то аmax > 0. Если же cosa – ksina = 0, т.е. 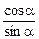 = ctga = k, то amax ® ¥. Это значит, что при таком k никакое ускорение призмы 1 не вызовет скольжения бруска 2. Но в нашей задаче по условию ctga > k, поэтому значение amax – положительная и конечная величина.
= ctga = k, то amax ® ¥. Это значит, что при таком k никакое ускорение призмы 1 не вызовет скольжения бруска 2. Но в нашей задаче по условию ctga > k, поэтому значение amax – положительная и конечная величина.
Ответ: 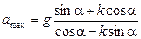 .
.
СТОП! Решение самостоятельно: В7, С2, С4, С5.
Задача 18.4. Через блок перекинута нить, к концам которой подвешены грузы массы т1 и т2 (т2 > т1) (рис. 18.7,а). Ось блока движется с ускорением a < g, направленным вниз. Найти ускорения грузов относительно блока и силу натяжения нити.
| т1 т2 a < g | Решение. Перейдем в н.с.о., связанную с блоком (рис. 18.7,б), тогда на тело 1 действует сила инерции 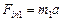 , направленная вверх, а на тело 2 – сила инерции , направленная вверх, а на тело 2 – сила инерции 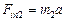 , также направленная вверх. При этом в н.с.о. «блок» тело 1 движется с ускорением , также направленная вверх. При этом в н.с.о. «блок» тело 1 движется с ускорением 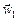 , направ- , направ-
|
| w = ? T = ? | |
ленным вверх, а тело 2 с таким же по величине ускорением 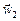 , направленным вниз: |
, направленным вниз: | 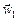 | = |
| = | 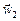 | = w. Силы натяжения нитей Т1 и Т2 равны: Т1 = Т2 = Т.
| = w. Силы натяжения нитей Т1 и Т2 равны: Т1 = Т2 = Т.
а) 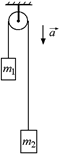 б)
б) 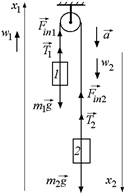 Рис. 18.7
Рис. 18.7
| Запишем второй закон Ньютона для каждого тела соответственно в проекциях на оси х1 и х2:
х1: т1а + Т – m1g = m1w, (1)
х2: т2g – Т – m2a = m2w. (2)
Сложив уравнения (1) и (2), находим w:
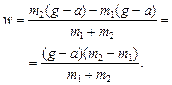 Подставив значение w в (1), найдем Т:
Подставив значение w в (1), найдем Т:
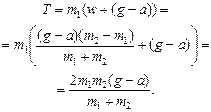 Ответ:
Ответ: 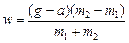 ; ;
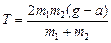 . .
|
СТОП! Решите самостоятельно: В8, С7, С8.
Задача 18.5. Найти ускорение системы грузов относительно стола, если этот стол находится в лифте, который поднимается вертикально вверх с ускорением а (рис. 18.8,а). Масса каждого груза т, коэффициент трения груза о стол μ < 1.
| а т μ < 1 | Решение. Перейдем в н.с.о. «лифт». Тогда на первое тело действуют силы 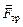 , , 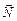 , , 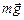 , , 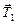 и и 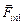 , а на второе , а на второе 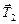 , , 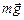 и и 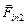 . Оба тела (в силу нерастяжимости нити) движутся с одинаковыми по модулю ускорениями . Оба тела (в силу нерастяжимости нити) движутся с одинаковыми по модулю ускорениями
|
| w = ? | |
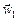 и
и 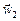 :
: 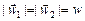 (рис. 18.8,б). При этом Т1 = Т2 = Т, Fтр = μN, Fin1 = Fin2 = та.
(рис. 18.8,б). При этом Т1 = Т2 = Т, Fтр = μN, Fin1 = Fin2 = та.
Запишем второй закон Ньютона в проекциях на оси: для первого тела – х1 и у1, для второго тела – х2.
х1: Т – μN = mw; (1)
у1: N – mg – ma = 0; (2)
х2: ma + mg – T = mw. (3)
Из (2) имеем
N = m(а + g) Þ (1) Þ
Т – μm(a + g) = mw. (4)
Сложив уравнения (4) и (3), получим
ma + mg – μm(a + g) = 2mw Þ
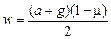 .
Ответ: .
Ответ: 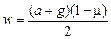 . .
|
a) 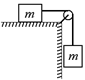
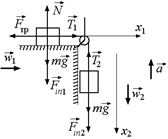 б)
Рис. 18.8
б)
Рис. 18.8
|
СТОП! Решите самостоятельно: С10, С12, С13.
Дата добавления: 2016-04-11; просмотров: 1996;
