Вес тела на экваторе и на полюсе
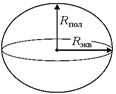Рис. 17.8
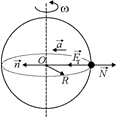Рис. 17.9
| Автор: Как Вы считаете, где тело массой т = = 1 кг весит больше: на экваторе или на полюсе? Читатель: На полюсе. Потому что Земля как бы немного приплюснута с полюсов и полярный радиус меньше экваториального (рис. 17.8). Автор: Вы правы, «приплюснутость», конечно, есть, но только ли в этом дело? Допустим, что наша Земля – идеальный шар радиуса R. Где тогда больше вес: на экваторе или на полюсе? Читатель: Наверное, тогда вес будет одинаков? |
Автор: Давайте рассмотрим тело, лежащее на экваторе (рис. 17.9) на него действуют две силы: сила тяготения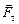 
( 
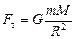) и сила нормальной реакции 
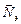. При этом наше тело движется с центростремительным ускорением 
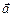(а = w2R, где w – угловая скорость вращения Земли, а R – ее радиус). Тогда второй закон Ньютона в проекции на ось 
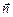имеет вид
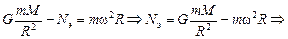
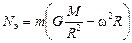. (17.12)
Поскольку на полюсе радиус вращения тела можно считать равным нулю, то
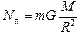. (17.3)
Как видите, Nп > Nэ!
Читатель: Но из формулы (17.12) следует, что если постепенно увеличивать w, то Nэ (а значит, и вес тела, так как Рэ = Nэ) будет уменьшаться, а в какой-то момент вообще станет равным нулю! Разве это возможно?
Автор: Вполне! Чтобы было понятно, решим задачу.
Задача 17.2. Какой продолжительности должны быть сутки на Земле, чтобы тела на экваторе были невесомыми?
| Р = 0 R = 6400 км | Решение. Приравняем нулю выражение (17.12) и получим
 .
|
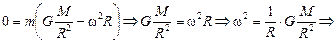
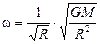| Т = ? | |
Так как по формуле (17.5)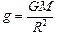 
, имеем 
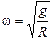. Тогда
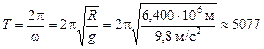с » 1 ч 24 мин.
Ответ: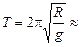 
1 ч 24 мин.
Заметим, что ускорение свободного падения относительно земной поверхности зависит от широты местности. И если бы сутки на Земле действительно длились 1 ч 24 мин, то на полюсе g равнялось бы по-прежнему 9,8 м/с2, а на экваторе g было бы равно нулю.
СТОП! Решите самостоятельно: В8, В9, С6.
Читатель: По-моему, есть еще один способ уменьшить вес тела на экваторе: надо быстро двигаться с запада на восток! Тогда угловая скорость тела увеличится на величину υ/R (где υ – его скорость, а R – радиус Земли), а значит, вес согласно формуле (17.12) уменьшится!
Автор: Совершенно верно. Замечу только, что если двигаться с востока на запад со скоростью, не превышающей wR, где w – угловая скорость вращения Земли, то вес будет, наоборот, увеличиваться.
СТОП! Решите самостоятельно: В11, В13.
Задача 18.3. Двойная планета. Определить угловую скорость w вращения двухпланетной системы. Массы планет М1 и М2, расстояние между центрами R. Найти также ускорения, с которыми движутся планеты.
| М1, М2, R | Решение. Планеты вращаются около некоторой точки О – центра масс системы. Пусть радиус вращения первой планеты R1, а второй – R2 (рис. 17.10). Тогда R1 + R2 = R. |
| w = ? а1 = ? а2 = ? | |
Запишем второй закон Ньютона в проекции на нормаль для каждой из планет:
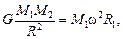(1) 
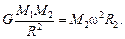(2)
Сложив почленно (1) и (2), получим
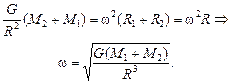
Ускорения планет найдем из второго закона Ньютона, ведь на каждую планету действует единственная сила тяготения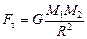 
, поэтому 
, 
.
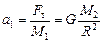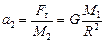Ответ: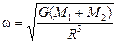 
; 
; 
.
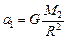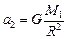СТОП! решите самостоятельно: С8, С9.
Дата добавления: 2016-04-11; просмотров: 6047;