Первая космическая скорость

Автор: Как Вы считаете, можно ли неограниченно долго падать на Землю и при этом… не упасть на нее?

Читатель: Думаю, нет. В конце концов, все, что падает, упадет.

Автор: А как же искусственные спутники Земли? Они ведь все время нахо­дятся в свободном падении.

Читатель: Спутники? Но они же вращаются вокруг Земли, а не падают на нее!

Автор: Под падением я понимаю движение под действием одной-единственной силы – силы тяжести. А на спутник с выключенными двигателями никакие другие силы как раз и не действуют. Так что движение спутника — это типичное свободное падение.

Читатель: Тогда я не понимаю, как же спутникам удается удержаться на орбите…

Автор: Вас удивляет, что сила тяжести тянет спутник к центру Земли, а он движется по окружности? А посмотрите на шарик, который вращают на нити в горизонтальной плоскости (рис. 17.1): сила натяжения нити все время на­правлена к центру окружности, а шарик движется по окружности. На спутник же вместо силы натяжения нити действует сила тяжести (рис. 17.2).

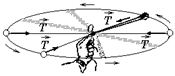Рис. 17.1

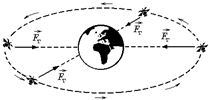Рис. 17.2

Чтобы было понятнее, сделаем такой мысленный эксперимент. Подни­мемся на очень высокую башню высотой километров, эдак, в сто (на этой высоте сила сопротивления воздуха уже практически отсутствует) и будем бросать с башни камешки, как показано на рис. 17.3. Чем с большей ско­ростью мы бросим камешек, тем дальше упадет он от основания башни. Наконец, при какой-то определенной скорости он вообще не упадет на землю, а вернется к нам с противоположной стороны.

Тут необходима осторож­ность: учитывая, что скорость такого камешка должна быть раз в 10 больше скорости артиллерийского снаряда, то последствия могут быть... сами по­нимаете. А скорость такого камешка как раз и называется первой космичес­кой. Сформулируем это четче.

Первой космической скоростью называется скорость, которую надо сооб­щить телу, чтобы оно стало спутником Земли и двигалось по круговой орбите на небольшой по сравнению с радиусом Земли высоте.

Давайте сразу и вычислим первую космическую скорость υ_I. Так как тело находится на небольшой высоте h << R, то ускорение свободного падения будем считать равным g = 9,8 м/с². Единственная сила, которая действует на тело, движущееся по круговой орбите вокруг Земли, – это сила тяжести 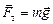. Она-то и сообщает телу центростремительное ускорение 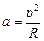, где R – радиус Земли.

По второму закону Ньютона:

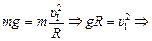
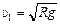. (17.9)

Подставим численные значения (R = 6,400×10⁶ м, g = 9,8 м/с²), получим:

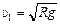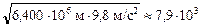= м/с = 7,9 км/с.

Запомним: первая космическая скорость равна υ_I = 7,9 км/с.

Заметим, что по формуле (17.9) можно вычислить первую космическую скорость не только для Земли, но и для любой другой планеты.

Если в формулу (17.9) подставить значение g из формулы (17.5), получим:

=

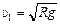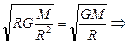
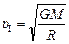. (17.10)

Если в формулу (17.9) подставить значение g из формулы (17.6), получим:

= =

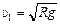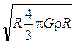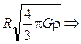
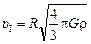. (17.11)

Формулы (17.10) и (17.11) можно использовать при решении задач.

Читатель: А что будет, если камешку на рис. 17.3 сообщить скорость υ > 7,9 км/с?

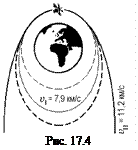Автор: При скорости, большей первой космической, траектория камешка (или космической станции) из окружности превратится в эллипс, который по мере увеличения скорости будет становиться все более вытянутым (рис. 17.4). Наконец, при скорости υ = 11,2 км/с, которую называют второй космической, траектория тела из эллипса превратится в параболу и тело навсегда покинет пределы земного тяготения.