ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ

Природа тока в металлах

Опыты показывают, что ток в металлах не связан с пе­ремещением атомов. Например, когда ток идет из медного провода в алюминиевый, то не происходит перехода атомов меди в алюминий или атомов алюминия в медь. В одном из опытов ток в подобной цепи поддерживался в течение года. Тщательные исследования показали, что никаких хими­ческих изменений в проводах не произошло (сверх незначи­тельной диффузии атомов, происходящей и при отсутствии тока). Если считать, что носителями тока в металле могут быть либо атомы, либо электроны, то эти опыты надо счи­тать свидетельством того, что носителями тока в металлах являются электроны. Таким образом, надо признать, что в металлах часть атомных электронов отрывается от атомов и способна перемещаться независимо от них. Эти электроны называют свободными.

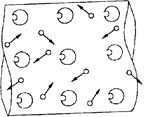Рис. 18.1

Итак, любой металл состоит из ионов, распо­ложенных в узлах кристаллической решетки, и свободных электронов, беспорядочно движущихся между ионами (рис. 18.1). Число свободных электронов огромно – по по­рядку величины их концентрация (т. е. число их на единицу объема) такая же, как и концентрация атомов.

В одном моле металла содержится N_А = 6,02×10²³ свободных электронов (если считать, что на один атом приходится ровно один свободный электрон).

Если создать в металле поле напряженностью Е, то на каждый электрон будет действовать со стороны поля сила F = eE.

Если бы электроны двигались в вакууме, то их скорость направленного движения непрерывно росла бы. Но в металлах они сталкиваются с ионами, отдавая им накопленную энергию. Затем они снова разгоняются электрическим полем, снова тормозятся ионами и т. д. Таким образом, максимальная, а стало быть, и сред­няя скорость направленного движения оказывается ограни­ченной.

СТОП! Решите самостоятельно: А1, В1, В2.

Связь силы тока со скоростью

Движения зарядов

Чем больше скорость направленного движения сво­бодных электронов, тем больший заряд проходит в единицу времени через данное сечение. Выведем точную формулу, связывающую эти величины. Докажем, что

I = enυS, (18.1)

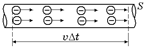Рис. 18.2

где е – заряд электрона; п – концентрация свободных электронов (их число в единице объема); S – площадь поперечного сечения проводника; υ – средняя скорость на­правленного движения электронов.

Для вывода формулы рассчитаем, какой заряд Dq подойдет к данному сечению S за время Dt, и найдем силу тока 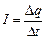. За время Dt к данному сечению успеют подойти электроны, отстоящие на расстояние υDt oт него (рис. 18.2), а также все более близкие электроны. Суммарный за­ряд этих электронов равен произведению заряда одно­го электрона на их число в объеме SυDt,т. e. Dq = епSυDt. Разделив обе части этого выражения на Dt, получим искомую формулу.

СТОП! Решите самостоятельно: В3, В4.