КОНДЕНСАТОРЫ И РЕЗИСТОРЫ
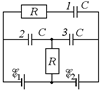 Рис. 17.1
Рис. 17.1
| Автор: Рассмотрим схему, состоящую из источников тока, резисторов (сопротивлений) и конденсаторов, представленную на рис. 17.1. Как Вы считаете, какие процессы будут происходить в такой системе? Читатель: По-моему, включить в цепь конденсатор – это все равно, что разорвать цепь. Полу- |
чается, что наша цепь разорвана сразу в трех местах, поэтому тока в этой цепи быть не может.
Автор: Верно. А будут ли заряжены конденсаторы?
Читатель: Я думаю, да. Ведь они подключены к источникам тока.
Автор: А можно ли подсчитать заряды каждого конденсатора?
Читатель: Если бы не было резисторов, это было бы не сложно.
Автор: А чем Вам так уж сильно мешают резисторы? Вы же сами
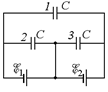 Рис. 17.2
Рис. 17.2
| сказали, что тока в данной схеме нигде нет, поэтому две точки, соединенные резисторами имеют одинаковый потенциал (если бы потенциалы были разными, через резисторы шел бы ток!). А значит, резисторы вполне можно заменить обычными соединительными проводами (рис. 17.2). |
Читатель: Тогда напряжения на конденсаторах легко найти:
U2 = õ1; U3 = õ2; U1 = õ1 + õ2.
Отсюда находим заряды конденсаторов:
q2 = õ1C; q3 = õ2C; q1 = (õ1 + õ2) C.
Автор: Совершенно верно!
СТОП! Решите самостоятельно: С1, С2.
Задача 17.1. Определить заряд на конденсаторе (рис. 17.3). Величины C, R1, R2, õ, r заданы.
| C R1, R2, õ r | Решение. Читатель: В этой схеме, по-моему, ток будет течь через сопротивление R1, а верхняя ветвь (с конденсатором) никакого значения иметь не будет. |  Рис. 17.3
Рис. 17.3
|
| q = ? | ||
Автор: То, что ток через верхнюю ветвь не потечет, безусловно, верно. Но скажите, будет ли равна нулю разность потенциалов между точками b и а.
Читатель: Нет, конечно! И ее легко найти:
jb – jа = IR1 = [õ/(R1 + r)]R1.
Автор: Верно! А нельзя ли тогда определить разность потенциалов между точками d и с, т.е. напряжение на нашем конденсаторе?
Читатель: Это совсем легко. Очевидно, что поскольку через верхнюю ветвь ток не течет, то jа = jс, jb = jd, следовательно:
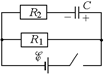 Рис. 17.4
Рис. 17.4
 а
а
 б
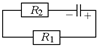
Рис. 17.5
б
Рис. 17.5
|
jd – jс = jb – ja = U = [õ/(R1 + r)]R1.
Автор: А зная напряжение на конденсаторе, можем ли мы найти заряд?
Читатель: Конечно: q = CU = CõR1/(R1 + r).
Автор: Задача решена!
Ответ: q = CõR1/(R1 + r).
Автор: Как Вы думаете, что произойдет, если разомкнуть нашу схему из только что решенной задачи ключом K (рис. 17.4)?
Читатель: В первое мгновение схема будет аналогична схеме, приведенной на рис. 17.5, а. Эту же схему можно для наглядности изобразить так, как показано на рис. 17.5, б, где
jВ – jА = U.
То есть мы получим два последовательно соединенных сопротивления, на концах которых разность потенциалов равна
jВ – jА = U = [õ/(R1 + r)]R1.
Тогда по закону Ома через сопротивления R1 и R2 пойдет ток
I = 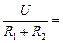 õ
õ 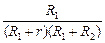 .
.
Автор: Верно! Этот ток будет постепенно убывать и станет равным нулю в тот момент, когда конденсатор окончательно разрядится.
СТОП! Решите самостоятельно: А1, В1–В3, С3.
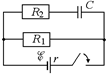 Рис. 17.6
Рис. 17.6
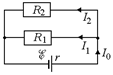 Рис. 17.7
Рис. 17.7
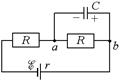
| Автор: А что произойдет, если в той же схеме, где конденсатор С первоначально не заряжен, замкнуть ключ K (рис. 17.6)?
Читатель: Я думаю, что в первый момент, когда конденсатор «готов» принимать на себя заряды, а поля внутри него еще нет, конденсатор как бы имеет «нулевое» сопротивление!
Автор: Совершенно верно! А значит, в первый момент после замыкания ключа наша схема эквивалентна схеме, показанной на рис. 17.7.
Читатель: Тогда через сопротивления R1 и R2 будут идти токи, которые нетрудно найти:
I0 = õ/(R0 + r) = õ / 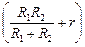 ; ;
|
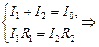
 ;
; 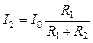 .
.
Автор: Совершенно верно! Ясно, что через очень небольшое время ток I2 станет равным нулю, а ток I1 примет значение I1 = õ/(R1 + r).
СТОП! Решите самостоятельно: С4.
 Задача 17.2. Вычислить напряжение и заряд на конденсаторе С (рис. 17.8). Величины С, R, õ, r заданы.
Задача 17.2. Вычислить напряжение и заряд на конденсаторе С (рис. 17.8). Величины С, R, õ, r заданы.
Рис. 17.8
| С, R õ, r | Решение. Ток через конденсатор не течет, поэтому для вычисления тока исходную схему можно заменить схемой на рис. 17.9. Тогда I = õ/(2R + r). | 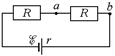 Рис. 17.9
Рис. 17.9
|
| U = ? q = ? | ||
Напряжение на конденсаторе
U = jb – jа = IR = õR /(2R + r).
Заряд конденсатора
q = CU = CõR /(2R + r).
Ответ: U = õ R /(2R + r); q = Cõ R /(2R + r).
СТОП! Решите самостоятельно: В5, В6,С5, С6.
Задача 17.3. Вычислить разность потенциалов между точками е и d (рис. 17.10). Величины õ, R, C заданы, внутреннее сопротивление источника равно нулю.
| õ R C | Решение. Примем потенциал в точке а равным нулю: jа = 0. Тогда потенциал в точке b jb = õ. На участке ab идет ток I = õ/(R + 2r) = I = õ/3R. | 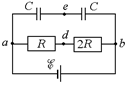 Рис. 17.10
Рис. 17.10
|
| jе – jd = ? | ||
Потенциал точки d равен напряжению на сопротивлении R:
jd = IR = (õ/3R)R = õ/3.
Так как верхняя ветвь схемы симметрична, то потенциал точки е равен jе = (jb – jа)/2 = (õ – 0)/2 = õ/2. Тогда искомая разность потенциалов jе – jd = õ/2 – õ/3 = õ/6.
Ответ: jе – jd = õ/6.
СТОП! Решите самостоятельно: С7–С9.
| Задача 17.4. Определить заряд на конденсаторе С (рис. 17.11). Величины õ и r заданы. |
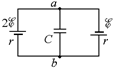 Рис. 17.11
Рис. 17.11
|
| õ, С, r | Решение. Сначала найдем ток. Для этого представим исходную схему в виде, показанном на рис. 17.12. Тогда: |
| q = ? | |
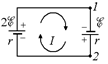 Рис. 17.12
Рис. 17.12
|
I = (2õ + õ)/(r + r) = 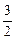 (õ/r);
(õ/r);
Тогда
j1 – j2 = jа – jb = õ – Ir =
= õ – 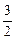 (õ/r) × r = –
(õ/r) × r = – 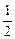 õ,
õ,
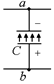 Рис. 17.13
Рис. 17.13
|
т.е. jа < jb. Это значит, что нижняя пластина конденсатора С заряжена положительно, а верхняя – отрицательно (рис. 17.13). Напряжение на конденсаторе
U = jb – jа = õ/2,
тогда заряд
q = CU = Cõ/2.
Ответ: q = õ 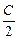 .
.
СТОП! Решите самостоятельно: В8, С10, С12.
Задача 17.5. Вычислить напряжение и заряд на конденсаторе С (рис. 17.14, а). Величины С, õ, R, r заданы.
| С õ R r | 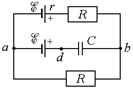 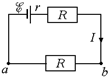 а б
Рис. 17.14
а б
Рис. 17.14
|
| U = ? q = ? | |
Решение. Сначала найдем ток, который протекает через сопротивления R. Для этого упростим исходную схему, «выкинув» из нее ветвь с конденсатором (рис. 17.14, б). По закону Ома сила тока
I = õ/(2R + r).
Теперь найдем разность потенциалов между точками b и а:
jb – jа = Ir = õR /(2R + r).
Если положить jа = 0, то
jb = õR /(2R + r).
Чтобы найти напряжение на конденсаторе, надо найти потенциал точки d (см. рис. 17.14, а). Очевидно, что
jd = jа + õ = 0 + õ = õ.
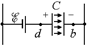 Рис. 17.15
Рис. 17.15
|
Заметим, что поскольку jd = õ больше, чем jb = õR /(2R + r), то при переходе от d к b потенциал уменьшается. Это значит, что поле внутри конденсатора направлено от d к b, следовательно, левая пластина заряжена положительно, а правая – отрицательно (рис. 17.15). Находим напряжение и заряд на конденсаторе:
U = jd – jb = õ – õ 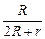 = õ
= õ 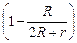 = õ
= õ 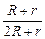 ;
;
q = CU = Cõ 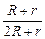 .
.
Ответ: U = õ 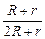 ; q = Cõ
; q = Cõ 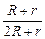 .
.
СТОП! Решите самостоятельно: В9, С11, С13.
Задача 17.6. Определить заряды на каждом конденсаторе (рис. 17.16). Величины õ, R, C заданы, внутренним сопротивлением источника пренебречь.
| õ С r | Решение. Если положить jd = = 0, то je = õ. Через сопротивления R и 2R течет ток I = õ/(R +2r) = õ/3R. Тогда напряжение на сопротивлении R равно UR = IR = (õ/3R)R = õ/3. | 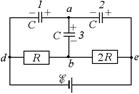 Рис. 17.16
Рис. 17.16
|
| q1 = ? q2 = ? q3 = ? | ||
Следовательно, потенциал точки b равен jb = UR = õ/3.
Найдем потенциал точки а. Поскольку на участке ead потенциал убывает, то правые пластины конденсаторов 2 и 1 заряжены положительно, а левые – отрицательно. Про знаки зарядов пластин конденсатора 3 определенно сказать нельзя, поэтому предположим, что его верхняя пластина заряжена положительно, а нижняя – отрицательно.
Пластины конденсаторов, примыкающие к узлу а, образуют единый электрически нейтральный проводник (рис. 17.17), поэтому справедливо
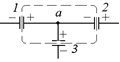 Рис. 17.17
Рис. 17.17
|
q1 + q3 – q2 = 0. (1)
С другой стороны,
q1 = jаС, (2)
q2= (jе – jа)С = (õ – jа)С, (3)
q3 = (jа – jb)С = (jа – õ/3)С. (4)
Подставив эти значения в (1), получим:
jаС + (jа – õ/3)С – (õ – jа)С = 0 Þ
Þ jа + jа – õ/3 – õ + jа = 0 Þ 3jа = 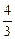 õ Þ jа =
õ Þ jа = 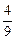 õ.
õ.
Подставляя полученное значение jа в (2)–(4), находим
q1 = 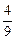 õС; q2 = (õ –
õС; q2 = (õ – 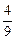 õ)С =
õ)С = 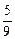 õС;
õС;
q3 = ( 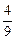 õ –
õ – 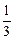 õ)С =
õ)С = 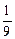 õС.
õС.
Заметим, что поскольку значение jа = 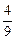 õ оказалось больше значения jb = õ/3, то знаки зарядов на пластинах конденсатора 3 мы указали верно.
õ оказалось больше значения jb = õ/3, то знаки зарядов на пластинах конденсатора 3 мы указали верно.
Ответ: q1 = 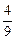 õС; q2 =
õС; q2 = 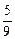 õС; q3 =
õС; q3 = 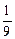 õС.
õС.
СТОП! Решите самостоятельно: В10, С14, С15.
Дата добавления: 2016-04-11; просмотров: 1705;
