Источников тока и конденсаторов
Задача 16.9. Найти заряд на каждом конденсаторе С1, С2 и С3, схема соединения которых дана на рис. 16.13. ЭДС батареи равна õ.
| С1 С2 С3 õ | 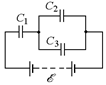 Рис. 16.13
Рис. 16.13
| Решение. Найдем общую емкость С0 системы конденсаторов:
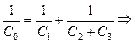
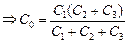 . .
|
| q1 = ? q2 = ? q3 = ? | ||
Тогда заряд «эквивалентного» конденсатора С0 равен
q = õC0 = õ 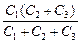 .
.
Этой же величине равен заряд q1:
q1 = q = õC0 = õ 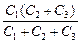 .
.
Так как конденсаторы С2 и С3 соединены параллельно, то
q2 + q3 = q; (1)
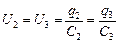 . (2)
. (2)
Из равенств (1) и (2) нетрудно получить
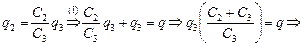
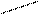
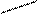
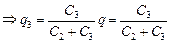 õ
õ 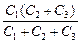 = õ
= õ 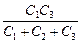 .
.
Аналогично, q2 = õ 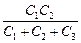 .
.
Ответ: q1= õ 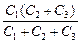 ; q2 = õ
; q2 = õ 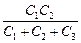 ;
;
q3 = õ 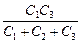 .
.
СТОП! Решите самостоятельно: В15, С15, С16, D3.
Задача 16.10.На рис. 16.14 показана схема соединения конденсаторов. Найти напряжение на каждом конденсаторе.
| õ1, õ2 С1, С2, С3 | Решение. Иногда встречаются такие соединения конденсаторов, которые не сводятся к совокупности параллельных и последовательных соединений. Как раз с таким примером разветвленной цепи мы сталкиваемся в условии этой задачи. | 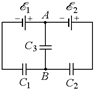 Рис. 16.14
Рис. 16.14
|
| U1 = ? U2 = ? U3 = ? | ||
Каким образом найти напряжения на конденсаторах в этом случае?
Попробуем составить необходимые уравнения. Прежде всего, отметим, что знаки заряда каждой пластины конденсаторов С1и С2 можно указать сразу: соединенная с полюсом источника обкладка конденсатора будет иметь заряд того же знака, что и соответствующий полюс. А вот с конденсатором С3дело обстоит сложнее, ибо одна из его обкладок, как видно из рис. 16.14, соединена одновременно и с положительным полюсом одного источника, и с отрицательным полюсом другого. Поэтому сразу указать знак заряда этой обкладки невозможно. Ясно лишь, что заряд этой обкладки может быть и положительным, и отрицательным в зависимости от того, какая разность потенциалов установилась бы между точками А и В вотсутствие конденсатора С3. Но можно не терять время на выяснение этого вопроса, а просто предположить, что заряд этой обкладки имеет определенный знак, например, положительный, т. е. знаки зарядов всех обкладок такие, как показано на рис. 16.15. Если мы не угадали знака заряда, то из правильно составленных уравнений для напряжения U3получится не положительное, а отрицательное значение.
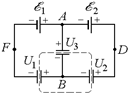 Рис. 16.15
Рис. 16.15
|
Теперь можно написать уравнения, связывающие напряжения на конденсаторах с электродвижущими силами источников. Рассмотрим, например, разность потенциалов между точками D и F на рис. 16.15. С одной стороны, эта разность потенциалов равна сумме ЭДС õ1 + õ2, с другой – сумме напряжений на конденсаторах С1и С2. Поэтому
U1 + U2 = õ1 + õ2. (1)
Точно так же напряжение между точками А и F с одной стороны равно ЭДС õ1, с другой – сумме напряжений на конденсаторах С1и С3:
U1 + U3 = õ1. (2)
Двух написанных уравнений (1) и (2) недостаточно для определения трех неизвестных напряжений U1, U2и U3. Поэтому нужно написать еще одно уравнение. Если мы попытаемся, рассуждая так же, как и раньше, рассмотреть разность потенциалов между точками D и А, то придем к уравнению
U2 – U3 = õ2. (3)
Однако легко видеть, что это уравнение не поможет в определении неизвестных, так как оно является следствием двух написанных ранее уравнений: вычитая почленно уравнение (2) из (1), получим уравнение (3).
Третье независимое уравнение можно получить так же, как и в случае последовательного соединения конденсаторов, учитывая условие электронейтральности соединенных между собой обкладок конденсаторов, не имеющих контакта с полюсами источников. Эта электронейтральная система обкладок обведена пунктиром на рис. 16.15. В отличие от случая последовательного соединения конденсаторов, это условие приводит не к равенству их зарядов, а к требованию равенства нулю алгебраической суммы зарядов указанных обкладок:
C1U1 – C2U2 – C3U3 = 0. (4)
Уравнение (4) вместе с любыми двумя из уравнений (1), (2) и (3) образует систему для нахождения неизвестных U1, U2и U3. На этом «физика» кончается и начинается «алгебра».
Выразим, например, U3из уравнения (4)
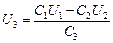 (5)
(5)
и подставим в (2), получим 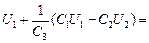 õ1 Þ
õ1 Þ
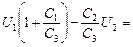 õ1. (6)
õ1. (6)
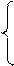 Составим систему из уравнений (6) и (1):
Составим систему из уравнений (6) и (1):
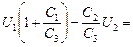 õ1;
U2 + U3 = õ1 + õ2. (1) õ1;
U2 + U3 = õ1 + õ2. (1)
|
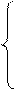 Умножим уравнение (1) на
Умножим уравнение (1) на 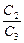 :
:
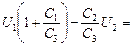 õ1; õ1;
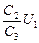 + + 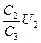 = = 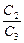 (õ1 + õ2). (õ1 + õ2).
|
Сложим почленно получившиеся равенства, получим
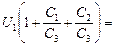 õ1 +
õ1 + 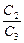 (õ1 + õ2) Þ
(õ1 + õ2) Þ
Þ 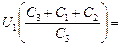
| õ1C3 + C2(õ1 + õ2) | Þ | |||
| С3 | |||||
Þ 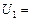
| C3õ1 + C2(õ1 + õ2) | . (7) | |||
| С1 + С2 + С3 | |||||
Подставив (7) в (2), найдем U3:
| U1 + U3 = õ1 Þ U3 = õ1 – U1 = õ1 – | C3õ1 + C2(õ1 + õ2) | Þ | ||
| С1 + С2 + С3 | ||||
| U3 = | C1õ1 – C2õ2 | . (8) | ||
| С1 + С2 + С3 | ||||
Из (1) находим U2:
| U1 + U2 = õ1 + õ2 Þ | C3õ1+ C2(õ1 + õ2) | + U2 = õ1 + õ2 Þ | |||||
| С1 + С2 + С3 | |||||||
| Þ U2 = (õ1 + õ2) – | C3õ1 + C2(õ1 + õ2) | = | |||||
| С1 + С2 + С3 | |||||||
| = | C1(õ1 + õ2) + C2(õ1 + õ2) + C3(õ1 + õ2) – C3õ1 – C2(õ1 + õ2) | Þ | |||||
| С1 + С2 + С3 | |||||||
| U2 = | C3õ2 + C1(õ1 + õ2) | . (9) | ||
| С1 + С2 + С3 | ||||
| Ответ: U1= | C3õ1 + C2(õ1 + õ2) | ; | ||
| С1 + С2 + С3 | ||||
| U2= | C3õ2 + C1(õ1 + õ2) | ; U3= | C1õ1 – C2õ2 | . |
| С1 + С2 + С3 | С1 + С2 + С3 |
Проанализируем полученные результаты.
Заметим, что значения U1и U2получаются положительными при любых значениях ЭДС и емкостей конденсаторов. Это значит, что знаки зарядов обкладок конденсаторов С1 и С2 действительно всегда такие, как указано на рис. 16.15. Значение величины U3,как видно из формулы (8), может быть и положительным, и отрицательным. Если C1õ1 > C2õ2, то U3 > 0, и знаки зарядов обкладок конденсатора С3будут такими, как показано на рис. 16.15. Если же С1õ1 < C2õ2, то U3 < 0. Это означает, что полярность напряжения на конденсаторе С3будет противоположной указанной на рис. 16.15.
Полезно проверить правильность полученных результатов в очевидных предельных и частных случаях. Во-первых, в симметричной схеме, когда õ1 = õ2 и C1 = C2, напряжение U3между точками А и В должно быть равно нулю, а напряжения U1и U2должны быть одинаковыми и равными ЭДС источника õ. Видно, что формулы (7)–(9) приводят в этом случае именно к такому результату.
Во-вторых, при С3 = 0,что соответствует отсутствию этого конденсатора, мы имеем последовательное соединение конденсаторов C1и С2 (рис. 16.16).
В этом случае
U1 = (õ1 + õ2) 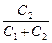 ; U2 = (õ1 + õ2)
; U2 = (õ1 + õ2) 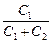 .
.
| При этом выполняется условие q1 = q2: C1U1 = C2U2. Наконец, случай С3 ® ¥ соответствует соединению точек А и В проводником (рис. 16.17). При этом напряжение на каждом конденсаторе равно ЭДС того источника, параллельно с которым он соединен: U1 = õ1, U2 = õ2. Именно это и получается из формул (7) и (8), так как при С3 ® ¥ в числителях и знаменателях этих формул можно пренебречь слагаемыми, не содержащими С3. Напряжение U3, как видно из (8), при этом стремится к нулю. СТОП! Решите самостоятельно: С18, С19. | 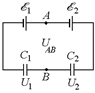 Рис. 16.16
Рис. 16.16
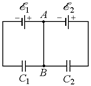 Рис. 16.17
Рис. 16.17
|
Схемы с «ключами»
Задача 16.11. Четыре одинаковых конденсатора емкостью С = = 5 мкФ каждый подключены к источнику тока с ЭДС õ = 2 В, как показано на рис. 16.18. Определить, насколько изменится заряд на конденсаторе С2 после замыкания ключа K.
| С = 5 мкФ õ = 2 В | Решение.Найдем общую емкость батареи до замыкания ключа:
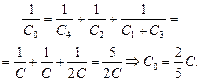
| 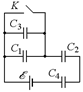 Рис. 16.18
Рис. 16.18
|
| Dq = ? | ||
Тогда заряд на конденсаторе С2 равен
q = С0õ = 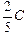 õ.
õ.
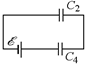 Рис. 16.19
Рис. 16.19
|
После замыкания ключа схема будет эквивалентна схеме, показанной на рис. 16.19 (конденсаторы С1 и С3 разрядятся и перестанут играть какую-либо роль). Теперь общая емкость будет равна
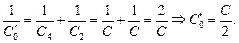
Тогда заряд на конденсаторе
q¢ = õ 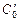 = õ
= õ 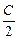 .
.
Находим изменение заряда на конденсаторе С2:
Dq = q¢ – q = 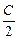 õ –
õ – 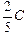 õ =
õ = 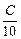 õ =
õ = 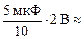 1 мкКл.
1 мкКл.
Ответ: Dq = 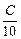 õ » 1 мкКл.
õ » 1 мкКл.
СТОП! Решите самостоятельно: В16, С20, С21.
Задача 16.12. Определить, какой заряд пройдет через источник тока и через проводник, соединяющий точки а и b при замыкании ключа. (рис. 16.20). Известно, что С1 = С2 = С3 = С; С4 = 2С; ЭДС равна õ.
| õ, С | Решение. 1. Найдем общую емкость и заряд батареи до замыкания ключа (рис. 16.21,а):
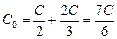 ; q0 = С0õ = ; q0 = С0õ = 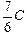 õ.
Теперь найдем общую емкость и заряд батареи после замыкания ключа (рис. 16.21,б): õ.
Теперь найдем общую емкость и заряд батареи после замыкания ключа (рис. 16.21,б):
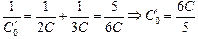 ;
q¢ = õ ;
q¢ = õ 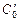 = = 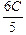 õ. õ.
|
| qи = ? qп = ? | |
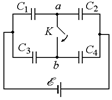 Рис. 16.20
Рис. 16.20
|
Следовательно, через источник прошел дополнительный заряд
qu = 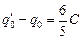 õ –
õ – 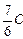 õ =
õ = 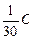 õ.
õ.
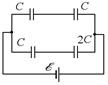 а
а
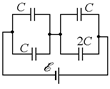 б
Рис. 16.21
б
Рис. 16.21
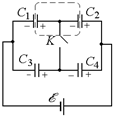 Рис. 16.22
Рис. 16.22
|
2. Определим общий заряд правой обкладки конденсатора С1 и левой обкладки конденсатора С2 до и после замыкания ключа (рис. 16.22).
До замыкания ключа эти обкладки составляют единый электрически нейтральный проводник, а значит, их общий заряд равен нулю: q12 = 0.
После замыкания (как мы уже выяснили) общий заряд конденсаторов С1 и С3 равен 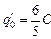 õ, этой же величине равен общий заряд конденсаторов С1 и С4:
õ, этой же величине равен общий заряд конденсаторов С1 и С4:
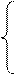
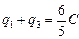 õ;
õ;
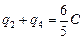 õ.
õ.
В силу того, что С1 = С3, заряды между конденсаторами С1 и С3 распределяются поровну:
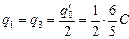 õ =
õ = 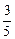 Сõ.
Сõ.
Поскольку конденсаторы С2 и С4 после замыкания соединены параллельно, напряжения на них равны, поэтому
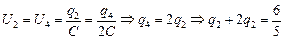 Сõ Þ
Сõ Þ
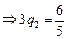 Сõ Þ
Сõ Þ 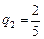 Сõ.
Сõ.
Поскольку заряд правой пластины конденсатора С1 положительный, а левой пластины конденсатора С2 – отрицательный, то их общий заряд равен
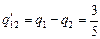 Сõ –
Сõ – 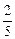 Сõ =
Сõ = 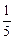 Сõ.
Сõ.
Именно этот заряд и протечет через проводник после замыкания ключа
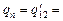
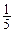 Сõ.
Сõ.
Ответ: qu = 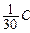 õ;
õ; 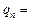
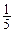 Сõ.
Сõ.
СТОП! Решите самостоятельно: С22, С23, D4, D5.
Задача 16.13.Какое количество тепла выделится при замыкании ключа K в схеме на рис. 16.23? ЭДС источника равна õ, емкости конденсаторов одинаковы и равны С.
| õ С | Решение. Общая емкость двух последовательно соединенных конденсаторов равна С0 = С/2, а их начальная энергия 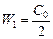 õ2 = õ2 = 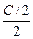 õ2 = õ2 = 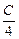 õ2. õ2.
|
| Q = ? | |
После замыкания ключа схема будет эквивалентной схеме, приведенной на рис. 16.24. Энергия конденсатора будет равна
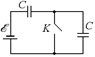 Рис. 16.23
Рис. 16.23
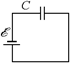 Рис. 16.24
Рис. 16.24
|
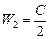 õ2.
õ2.
При этом после замыкания батарейка «протолкнула» по цепи дополнительный заряд
Dq = Cõ – C0õ = Cõ – 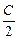 õ =
õ = 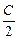 õ.
õ.
При этом она совершила работу
А = Dqõ = 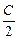 õ×õ =
õ×õ = 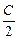 õ2.
õ2.
Эта работа пошла, с одной стороны, на увеличение энергии конденсаторов, а с другой – на выделение тепла:
А = (W2 – W1) + Q Þ
Þ 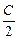 õ2 =
õ2 = 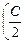 õ2 – õ2
õ2 – õ2 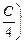 + Q Þ Q =
+ Q Þ Q = 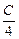 õ2.
õ2.
Это тепло частично выделится в соединительных проводах, кроме того, при замыкании проскочит искра – и излучится электромагнитная волна, будет слышен звук, значит, и звуковая волна образуется тоже.
Ответ: Q = 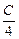 õ2.
õ2.
СТОП! Решите самостоятельно: С24, С25, D6.
Дата добавления: 2016-04-11; просмотров: 2667;
