Конденсаторов и источников тока
Задача 16.6. Вычислить разность потенциалов между точками а и b (рис. 16.10). Величины õ и С заданы.
| õ С | Решение. Так как цепь разомкнута, то напряжение между точками О и D равно õ. Пусть потенциал точки О равен нулю: jО = 0, тогда потенциал точки |
| jа – jb = ? |
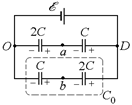Рис. 16.10
|
D равен õ: jD = õ. Чтобы ответить на вопрос задачи, надо вычислить потенциалы точек а и b. Заметим, что общая емкость С0 нижней цепочки равна общей емкости верхней цепочки: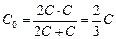 
, отсюда находим заряд на каждом конденсаторе:
q = õС0 =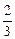 
õС.
Тогда
jа =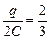 
õС : 2С = õ/3; jb = 
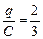õС : С = 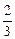õ;
jа – jb = õ/3 – 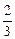õ = –õ/3,
т.е. потенциал точки а меньше потенциала точки b на õ/3.
Ответ: jа – jb = –õ/3.
СТОП! Решите самостоятельно: В10, В11, С11.
Задача 16.7. Определить разность потенциалов между точками а и b (рис. 16.11). Величины õ и С заданы.
| õ С | Решение. Пусть в точке О потенциал равен нулю: jО = 0, тогда jb = õ и jD = 3õ. Остается найти потенциал точки а. Для этого найдем заряды на конденсаторах. |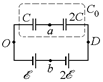 
Рис. 16.11
|
| jа – jb = ? | ||
Общая емкость конденсаторов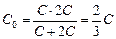 
, отсюда:
q = 3õС0 = 3õ 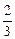С = 2õС.
Тогда jа =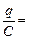 
2õС : С = 2õ Þ jа – jb = 2õ – õ = õ.
Ответ: jа – jb = õ.
СТОП! Решите самостоятельно: В12, В13, С12.
Задача 16.8. Определите заряды на конденсаторах (рис. 16.12), если величины õ и С заданы.
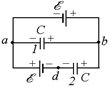Рис. 16.12
| ||
| õ С | Решение. Пусть ja = 0, тогда jb = = +õ, jd = –õ. Соответственно напряжение на конденсаторе 1: U1 = jb = õ, а на конденсаторе 2: U2 = jb – jd = õ – (–õ) = 2õ. Тогда q1 = U1C = õC, q2 = U2С = 2õС. | |
| q1 = ? q2 = ? | ||
Ответ: q1 = õC, q2 = 2õС.
СТОП! Решите самостоятельно: В14, С13, С14.
Дата добавления: 2016-04-11; просмотров: 836;