Конденсаторов и источников ЭДС

Задача 16.4. В схеме на рис. 16.5 источники тока имеют одинаковые ЭДС õ, а конденсаторы – емкости С₁ и С₂. Определить заряды и напряжения на каждом конденсаторе.

õ С1 С2	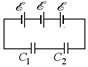Рис. 16.5	Решение. Заметим, что поскольку конденсаторы соединены последовательно, то их заряды равны: q1 = q2 = q. Заменим батарею источников тока на один эквивалентный источник, ЭДС
q1 = ? q2 = ? U1 = ? U2 = ?
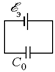Рис. 16.6
которого равна õэ = õ + õ – õ = õ. Заменим два последовательно соединенных конденсатора на один с емкостью 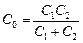(рис. 16.6). Тогда напряжение на конденсаторе U0 = õ, а заряд

q = U₀C₀ = õ .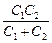

Итак, заряд q мы нашли. Вернемся к схеме на рис. 16.5:

q₁ = q₂ = q = C₁U₁ = C₂U₂ Þ

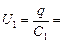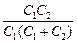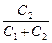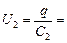õ = õ ;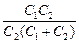

õ = õ .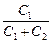

Ответ: q₁ = q₂ = õ 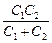; U₁ = õ 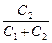; U₂ = õ .

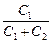Читатель: А изменится ли результат, если конденсаторы и источники тока будут «чередоваться» друг с другом?

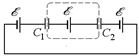Рис. 16.7

Автор: Ваш вопрос фактически сводится к следующему: можно ли заменить два конденсатора С₁ и С₂ на рис. 16.7 одним с емкостью С₀, такой, что 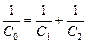? Давайте разберемся.

Конденсаторы С₁ и С₂ можно заменить на один конденсатор С₀, если выполняются два условия:

1) общее падение напряжения на них равно сумме падений напряжений на каждом (очевидно, что для схемы на рис. 16.7 это справедливо);

2) заряды обоих конденсаторов равны.

Рассмотрим участок цепи, объединяющий правую обкладку конденсатора С₁, источник ЭДС и левую обкладку конденсатора С₂ (на рис. 16.7). Если до подключения источника тока зарядов на конденсаторах не было, то после включения источника тока между двумя конденсаторами общий заряд участка останется равным нулю, поскольку источник тока в целом электрически нейтрален. А это значит, что по величине заряды на обкладках конденсаторов равны, т.е. q₁ = q₂.

Следовательно, при решении подобных задач совершенно неважно, в каком порядке расположены друг за другом конденсаторы и источники ЭДС.

СТОП! Решите самостоятельно: В7, С8, С9, D1.

Задача 16.5. Определить заряд конденсатора, если потенциалы точек А и В заданы (j_А > j_В), ЭДС источника тока õ, а емкость конденсатора С (рис. 16.8).

jА jВ С õ	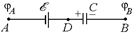Рис. 16.8 Решение. Автор: Как Вы считаете, правильно ли на рис. 16.8 указаны знаки зарядов обкладок конденсатора?
q = ?

Читатель: По условию j_А > j_В, но j_D = j_А + õ, т.е. j_D > j_В. Значит, на участке DB потенциал должен уменьшаться, а для этого напряженность поля внутри конденсатора должна быть направлена от D к В, от «плюса» к «минусу». Значит, знаки обкладок указаны верно.

Автор: Верно! В этом случае справедливо

j_В = j_А + õ – 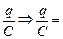j_А – j_В + õ Þ q = C[(j_А – j_В) + õ].

Ответ: q = C[(j_А – j_В) + õ].

Читатель: Получается, что если j_А < j_В и при этом (j_В – j_А) > õ, то значение q становится отрицательным. Чтобы это значило?

Рис. 16.9

Автор: Это значит, что знаки зарядов обкладок конденсатора должны поменяться местами, т.е. левая обкладка в этом случае будет заряжена отрицательно, а правая – положительно (рис. 16.9).

СТОП! Решите самостоятельно: В9, С10.