Ионное равновесие; электрохимический потенциал; профили потенциала и концентрации у границы раздела фаз; коэффициент распределения; двойной электрический слой

Транспорт ионов.

Движущая сила диффузии через мембрану в случае незаряженных частиц – разность химических потенциалов µ между областями, разделенными полупроницаемой мембраной (ПМ). Напомню, что µ=µ₀+RTlnC. Если через мембрану движутся заряженные частицы – например, ионы, - то это движение зависит не только от разности химических потенциалов, но и от разности электрических потенциалов. В этом случае пользуются электрохимическим потенциалом µ с чертой, которую не знаю как пставить. µ=µ₀+RTlnC+zFφ. Собственно, движущей силой для ионов является грдиент этого потенциала, который по определению является производной потенциала по напавлению dµ/dx.

Рассмотрим, что происходит, когда ион проникает в мембрану. Диэлектрическая постоянная ε_{липидов}=2-3, а ε_воды=81. Следовательно, энергия иона с радиусом r - E=e²/2rε – повышается в липидном слое! Следовательно, коэффициэнт распределения иона между водой и мембраной очень мал (напомню, что коэффициэнт распределения γ=С_лип/C_воды, это отношение концентраций иона ооооочень близке к границе с одной и с другой стороны). Он равен 10^-20-10^-30. Это значит, что в воде ооооооооооооочень много, а в мембрану проникает оооооооооочень мало.

Рассмотрим распределение электролита А⁺В^- между липидной (2) и водной (1) фазами. Пусть липофильность В^- больше, чем у А⁺. Поэтому вблизи границы в липидной фазе будет побольше анионов, следовательно, липидная фаза около границы будет иметь отрицательный заряд! Однако вдали от границы концентрации катионов и аноинов будут одинаковыми (потому что если ты уже в глубине липидной фазы, то в гробу все видали твою липофобность, тебе уже деваться некуда), так что соблюдается условие электронейтральности объемов(!) фаз (но не самой мембраны): C_A=C_B. В целом, концентрация обоих ионов ниже в липидной фазе, так как в ней у ионов горааздо выше энергия, им не выгодно (из-за разности в диэлектрических проницаемостях).

На рисунке: профили распределения потенциала и концентраций ионов А⁺ и В^- на границе раздела фаз I и II. Фаза I – водный раствор, а – распределение φ, б – распределение С. С₁ и С₂ – концентрации в объемах фаз I и II

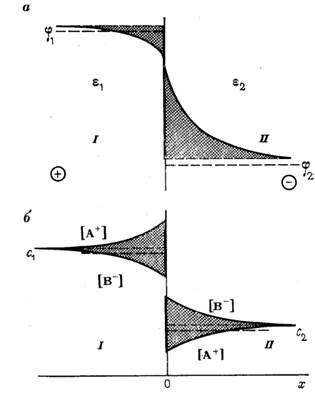
Кому не понятно, объясняю, че тут нарисовано. б – это концентрации. Мы видим, что вблизи границы А больше, чем В в водной фазе, а В больше, чем А в липидной. Но при этом и того, и другого в водной больше. По мере удаления от границы концентрации выравниваются до соблюдения электронейтральности в объемах фаз. А вблизи границ электронейтральности нет.

Пусть у нас установилось равновесие! Тогда электрохимические потенциалы фаз равны: µ_0А⁽¹⁾+RTlnC_A⁽¹⁾+Fφ⁽¹⁾= µ_0А⁽²⁾+RTlnC_A⁽²⁾+Fφ⁽²⁾. Ключевой момент в том, что СОВСЕМ вблизи границы φ⁽¹⁾= φ⁽²⁾ (видно из профиля, да и логично, совсем на границе потенциалы фаз равны). Следовательно, µ_0А⁽¹⁾+RTlnC_A⁽¹⁾= µ_0А⁽²⁾+RTlnC_A⁽²⁾. Вспоминаем, что γ=С_лип/C_воды, и пишем: ln γ_A=Δµ_0A/RT,(Δµ_0A= µ_0А⁽¹⁾- µ_0А⁽²⁾), аналогично для В.

При условии электронейтральности обеих фаз: C_В⁽¹⁾=С₁ и C_A⁽²⁾= C_В⁽²⁾=С₂, так что ln(C₂/C₁)=1/2* (ln γ_A + ln γ_B) (я этого не смог понять!) илиC₂/C₁=√( ln γ_A * ln γ_B).

Отношение концентраций электролита в фазах зависит от γ_A и от γ_B. Величина разности потенциалов Δφ=φ₁-φ₂ между фзами зависит от разности электрохимических потенциалов обоих ионов. Опять же, не в состоянии понять, почему: Δφ=φ₁-φ₂=1/2F*(Δµ_0B-µ_0A)=2F/RT*( ln γ_A - ln γ_B). Вывод: межфазная разность потенциалов возникает, только если коэффициенты распретеделения катионов и анионов различны (то есть разная липофильность, в данном случае).

Характер падения потенциала вблизи границы зависит от распределения ионов в двойной электрическом слое (двойной слой возникает у заряженных мембран. 1 слой – на самой мембране, т.к. она заряжена, второй – от электролита). Эмперический факт: потенциал падает при отдалении от границы экспоненциально: φ(х)=φ₀exp(χ|x|). χ – константа, зависящая от концентрации ионов в данной фазе и диэлектрической проницаемости. Потенциал падает в е раз на расстоянии x=1/ χ от границы. Величина λ=1/ χ – длина экранирования. Она падает при увеличении концентрации электролита в данной фазе (иными словами, при увеличении концентрации электролита в данной фазе потенциал падает быстрее при удалении от границы). Поэтому в разбавленных растворах толщина двойного диффузинного слоя – сотни ангстрем, а в концентрированных – единицы. Еще поэтому в липидном слое, где концентрация ниже, длина экранирования больше. Намного. Поэтому, если мембрана тонкая (ее толщина заметно меньше длины экранирования), то скачок потенциала внутри мембраны почти отсутсвует. Иными словами, в отсутсвии внешнего поля, потенциал тонкой мембраны постоянен по всей толщине! Поэтому значения потенциала в тонкой мембране не отличаются от уровня потенциала окружающих растворов на любом удалении от мембраны (не понял мысль...). Именно так и происходит в незаряженных бислойных липидных мембранах толщиной 70-100 ангстрем. Если приложить внешнее поле, то внутри мембраны потенциал будет меняться линейно, то есть градиент приложенного потенциала в мембране постоянен: dφ/dx=const.Однако, если поверхность мембраны заряжена, то около поверхности образуется двойной электрический слой. Противоионы электролита с одной стороны будут удерживаться мембраной электростатически, а сдругой – тепловое движение хочет их вернуть равномерно в лбъем электролита. Короче, потенциал на поверхности такой мембраны сложным образом зависит от плотности поверхностного заряда, равновесной концентрации электролита в растворе и температуры.

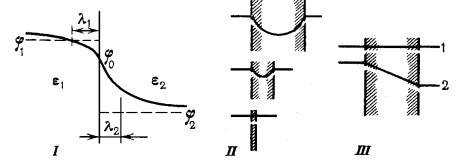
На рисунке профили распределения потенциала на границе раздела фаз – I. В мембранах разной толщины – II. В тонкой мембране в отсутсвии внешнего поля – III.1, и в присутсвии (т.е. при наложении разности электрических потенциалов) – III.2. φ₁ и φ₂ –электрические потенциалы в объеме фаз, φ₀ – на границе раздела фаз. Остальное в тексте.

Теперь немного про Доннановское равновесие.

Представим себе корыто, разделенное на две части – 1 и 2 – полупроницаемой мембраной (ПМ), через которую проходят и катионы, и анионы нашего электролита A⁺B^-, но не проходят фиксированные заряды Q (скажем, аминокослота какая-нить), находящиеся во второй части корыта. Направим ось x слева направо.

Напишем, чем равен электрохимический потенциал 1 и 2. µа₁= µа⁰+RTlnCа₁+zFφ₁, аналогично для 2.(Еще отныне забьем на z, так как будем считать, что у нас все одновалентное). И аналогично для аниона В.

Поскольку установилось равновесие, то Δµ= µ₁ - µ₂=0=>RT ln(C₁/C₂)+F(φ₁ – φ₂)=0 => φ₁ – φ₂=RT/F* ln(Ca₂/Ca₁)=- RT/F* ln(Cb₂/Cb₁) - уравнение Нернста. Вах, равновесный потенциал определяется соотношением концентраций электролитов в обеих фазах.

Если С_а1=С_а2=С_b1=C_b2=С, то Δφ=0. Из уравнения Нернста следует, что С_а2С_b2= С_а1С_b1=C².

Пусть во второй фазе есть фиксированные заряды – Q. Его влияение приведет к тому, что Δφ уже не равно нулю, капитан.=) Из условия электронейтральности первой фазы следует:

С_а1=С_b1=С, а для второй фазы С_а2+Q=C_b2. Значит, С_а2< C_b2, С_а2 C_b2= С_а1²=C², С_а2> С_а1. Значит, содержание Q во второй фазе компенсируется повышенном содержанием в ней анионов В и пониженном – катионов А. В этом случае возникает доннановская разность потенциалов: Δφ_D=φ₁ – φ₂=RTln(С_а1/ С_а2)= RT/F*ln(C/ С_а2)>0, где С_а2<C.