Лекция 7 Электростатика. Постоянный электрический ток

План

1. Расчет электрических полей методом суперпозиции. Поток вектора напряженности (электрического смещения). Теорема Остроградского-Гаусса для электростатического поля в вакууме.

2. Емкость конденсаторов различной геометрической конфигурации. Объемная плотность энергии электростатического поля.

3. Постоянный электрический ток. Разность потенциалов, электродвижущая сила, напряжение. Закон Ома для участка цепи. Классическая электронная теория электропроводности металлов. Закон Джоуля-Ленца. Правила Кирхгофа.

Тезисы

1. Напряженность электростатического поля в данной точке есть физическая вели­чина, определяемая силой, действующей на единичный положительный заряд, по­мещенный в эту точку поля: 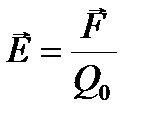Напряженность поля точечного заряда в вакууме 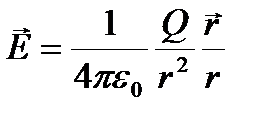или

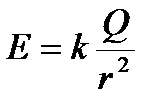
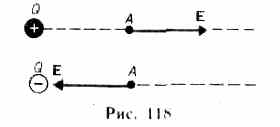
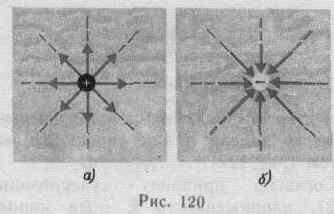
Единица напряженности электростати­ческого поля - ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл=1 В/м, где В (вольт) - единица потенциала электростатического поля. Линии напряжен­ности — линии, касательные к которым в каждой точке совпадают с направлением вектора Е. Принцип су­перпозиции: напряжен­ность результирующего поля, создавае­мого системой зарядов, равна геометриче­ской сумме напряженностей полей, со­здаваемых в данной точке каждым из зарядов в отдельности: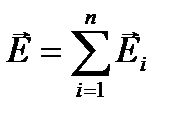

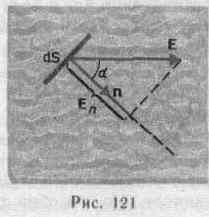
Ве­личина 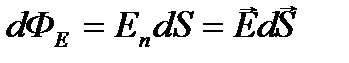называется потоком вектора напряженно­сти через площадку dS. Здесь dS == dSn — вектор, модуль которого равен dS, а направление совпадает с направ­лением нормали n к площадке. Единица потока вектора напряженно­сти электростатического поля— 1 В•м. Для произвольной замкнутой повер­хности S поток вектора Е через эту по­верхность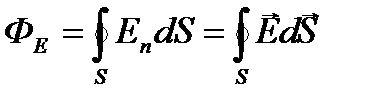

1. Напряженность поля на продолже­нии оси диполя в точке А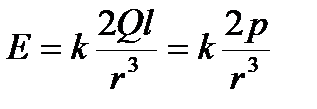

2. Напряженность поля на перпенди­куляре, восставленном к оси из его середи­ны, в точке В 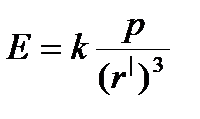, где r'— расстояние от точки В до середи­ны плеча диполя.

Теорема ОСТРОГРАДСКОГО-Га­усса для электростатического поля в ваку­уме: поток вектора напряженности элек­тростатического поля в вакууме сквозь произвольную замкнутую поверхность ра­вен алгебраической сумме заключенных внутри этой поверхности зарядов, делен­ной на e₀: 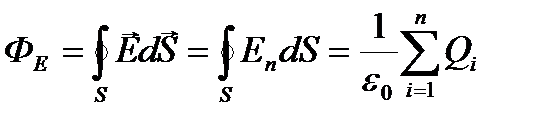или 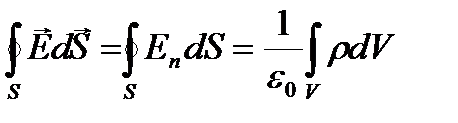Объемная плотность заряда 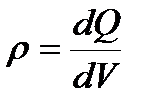, поверхностная плотность заряда 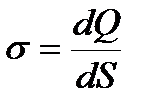, линейная плотность заряда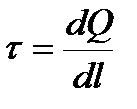

Применение теоремы ОСТРОГРАДСКОГО-Га­усса к расчету

некоторых электростатических полей в вакууме

1) Поле равномерно заряженной бесконечной плоскости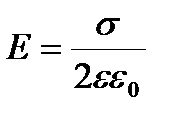

2) Поле двух бесконечных параллельных разноименно заряженных плоскостей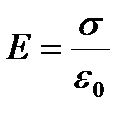

3) Поле равномерно заряженной сфериче­ской поверхности 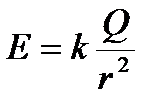, где r ≥R

4) Поле объемно заряженного шара 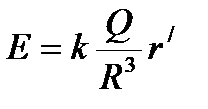, где r^/ ≤ R.

5) Поле равномерно заряженного бесконеч­ного цилиндра (нити) 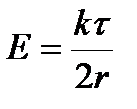, где r ≥ R

Рабо­та, совершаемая при перемещении элек­трического заряда во внешнем электроста­тическом поле по любому замкнутому пути L, равна нулю. Тогда 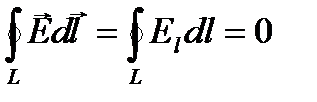, где интеграл 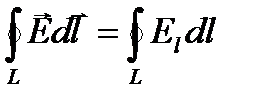называется циркуляцией вектора напряженности. Циркуляция вектора напряжен­ности электростатического поля вдоль лю­бого замкнутого контура равна нулю.

Работа сил электростатического поля 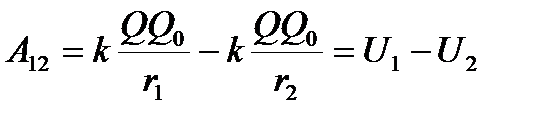Потенциальная энергия заряда Q₀, находящегося в поле заряда Q на расстоянии r от него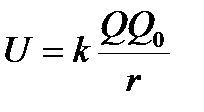

Потенциал в какой-либо точке элек­тростатического поля есть физическая ве­личина, определяемая потенциальной энергией единичного положительного за­ряда, помещенного в эту точку 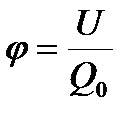Потенциал поля точечного заряда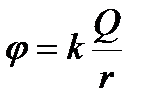

Работа, совершаемая силами элек­тростатического поля при перемещении заряда Q₀ из точки 1 в точку 2 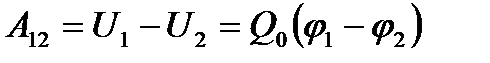Разность потенци­алов в электростатиче­ском поле определяется работой, соверша­емой силами поля при перемещении единичного положительного заряда. Еди­ница потенциала — вольт (В). Если поле создается несколькими за­рядами, то потенциал поля системы за­рядов равен алгебраической сумме потен­циалов полей всех этих зарядов: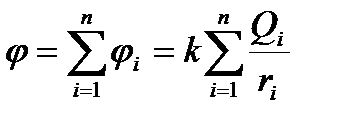

Напряженность поля равна гради­енту потенциала со знаком минус. Знак минус определяется тем, что вектор на­пряженности Е поля направлен в сторону убывания потенциала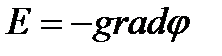

Вычисление разности потенциалов по напряженности поля

1) Разность потенциалов между точками, лежащими на расстояниях х₁, и x₂от плоскости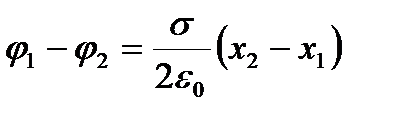

2) Разность потенциа­лов между плоскостями, расстояние между ко­торыми равно d: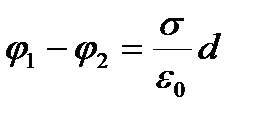

3) Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂от центра сферы (r₁>R, r₂>R)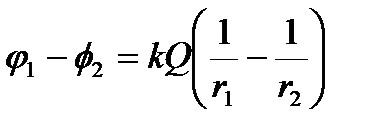

4) Внутри сферической поверхности потенциал всюду одинаков и равен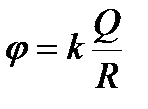

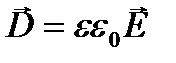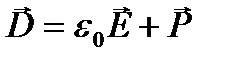2. Вектор элек­трического смещения или Единица электрического смещения — кулон на метр в квадрате (Кл/м²). Аналогично, как и поле Е, поле D изо­бражается с помощью линий электриче­ского смещения, направление и густота которых определяются точно так же, как и для линий напряженности. Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находят­ся связанные заряды, линии вектора D про­ходят не прерываясь.

Теорема Гаусса для электростатиче­ского поля в диэлектрике: поток вектора смещения электроста­тического поля в диэлектрике сквозь про­извольную замкнутую поверхность равен алгебраической сумме заключенных внут­ри этой поверхности свободных электриче­ских зарядов: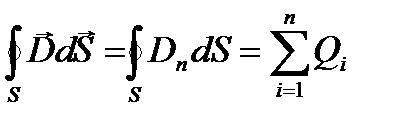

Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют различные потенциалы. Поэтому для уединённого проводника величину 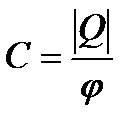называют электроёмкостью уединённого проводника. Ёмкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Единица электроёмкости – фарад (Ф); 1Ф – ёмкость такого уединённого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл.

Потенциал шара радиуса шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью 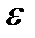, равен 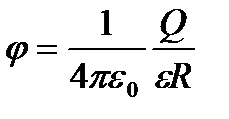, отсюда электроёмкость шара 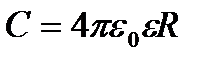. Из формулы вытекает также, что единица электрической постоянной 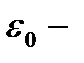фарад на метр (Ф/м) .

На практике необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой ёмкостью. Эти устройства получили название конденсаторов. Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (диэлектрике) заряды, причём ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, ослабляют поле, понижают потенциал, повышают его электроёмкость.

Конденсатор состоит из двух проводников, разделённых диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: две плоские пластины; два коаксиальных цилиндра; две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и заканчиваются на другой, поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноимёнными зарядами.

Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов между его обкладками: 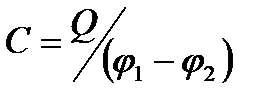Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q: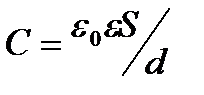

Емкость конденсаторов различной геометрической конфигурации.

1)Электроёмкость цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусам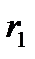и и 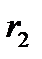, вставленных один в другой: 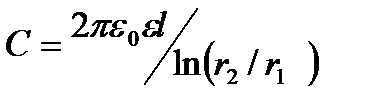2)Электроёмкость сферического конденсатора, состоящего из двух концентрических обкладок, разделённых сферическим слоем диэлектрика: 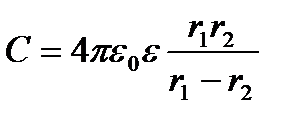Вывод: ёмкость конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками. Поэтому применение в качестве прослойки сегнетоэлектриков значительно увеличивает ёмкость конденсаторов.

Для увеличения ёмкости и варьирования её возможных значений конденсаторы соединяют в батареи, при этом используются их параллельное и последовательное соединения. У параллельно соединённых конденсаторов ёмкость батареи 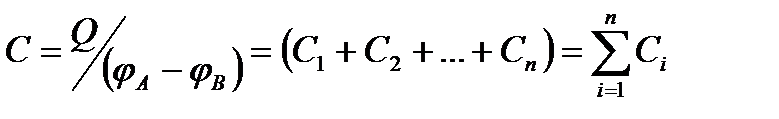, т.е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов. При последовательсном соединении конденсаторов заряды всех обкладок равны по модулю 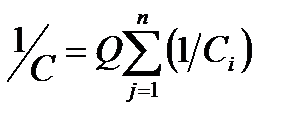, т.е. при последовательном соединении конденсаторов суммируются величины, обратные ёмкостям.

Электростатические силы взаимодействия консервативны, следовательно, система зарядов обладает потенциальной энергией. Потенциальная энергия системы двух неподвижных точечных зарядов Q₁ и Q₂, находящихся на расстоянии друг от друга: 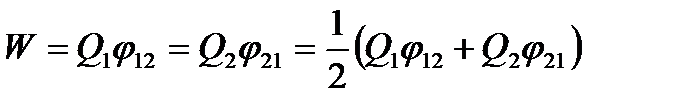. В случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна 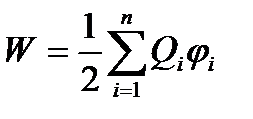, где 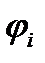- потенциал, создаваемый в той точке, где находится заряд Q_i, всеми зарядами, кроме i-гo.

Энергия заряженного конденсатора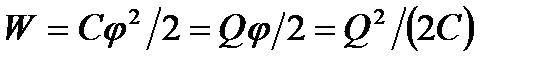

Энергия электростатического поля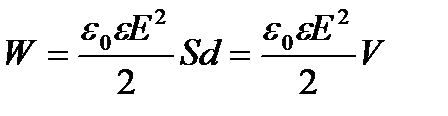

Объемная плотность энергии электростатического поля

(энергия единицы объема)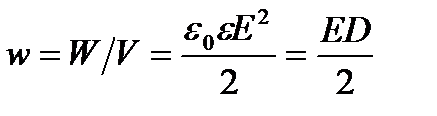

3. Носителями тока в металлах являются свободные электроны, т.е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной П.Друде и Х.Лоренцем. Идея опытов принажлежат С.Л.Мандельштаму и Н.Д.Папалекси. По значению удельного заряда носителей тока и по определенному ранее Р.Милликеном элементарному заряду было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны. Существование свободных электронов в металлах можно объяснить: при образовании кристаллической решетки металла валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Так, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя электронный газ.

Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие. По теории Друде - Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому можно найти среднюю скорость теплового движения электронов 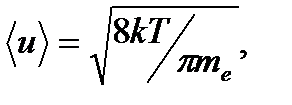которая для Т = 300 К равна 1,1*10 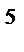м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.

При наложении внешнего электрического поля на металлический проводник, кроме теплового движения электронов, возникает их упорядоченное движение, т.е. возникает электрический ток. Среднюю скорость 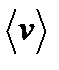упорядоченного движения электронов можно оценить: 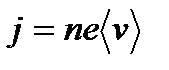. Выбрав допустимую плотность тока, например для медных проводов 10 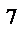А/м², получим, что при концентрации носителей тока 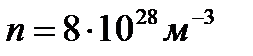средняя скорость 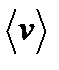упорядоченного движения равна 7,8*10 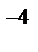м/с.

Закон Видемана-Франца: отношение теплопроводности ( 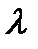) к удельной проводимости (γ) для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температур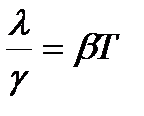е , где 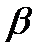- постоянная, не зависящая от рода металла. Элементарная классическая теория электропроводности металлов столкнулась еще с рядом трудностей при объяснении различных опытных данных: 1.Температурная зависимость сопротивления 2.Оценка средней длины свободного пробега электронов в металлах. 3.Теория металлов По закону Дюлонга-Пти теплоемкость одноатомного кристалла равна С = 3R. Однако наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.

Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. Сила тока – скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени 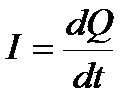Единица силы тока - ампер (А). Плотность тока - физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока 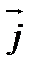= 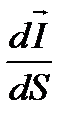Единица плотности тока - ампер на метр в квадрате (А/м²). 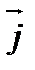= 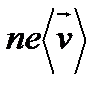или γ 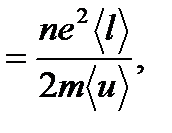где n – концентрация электронов, v – скорость их движения. Сила тока сквозь произвольную поверхность 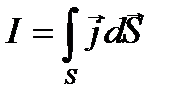, где 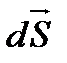= 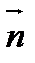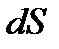. Напряжение - физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. 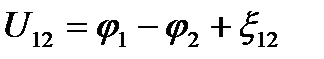Напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т.е. сторонние силы отсутствуют.

Закон Ома для однородного участка цепи (отсутствие источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника 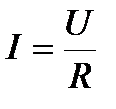. Единица сопротивления – ом (Ом). Электрическая проводимость проводника 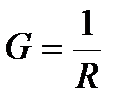Единица проводимости – сименс (См). Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника 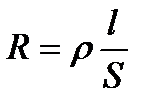, где ρ – удельное электрическое сопротивление. Единица удельного электрического сопротивления – ом*метр (Ом*м). Закон Ома в дифференциальной форме (связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке) 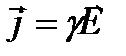. 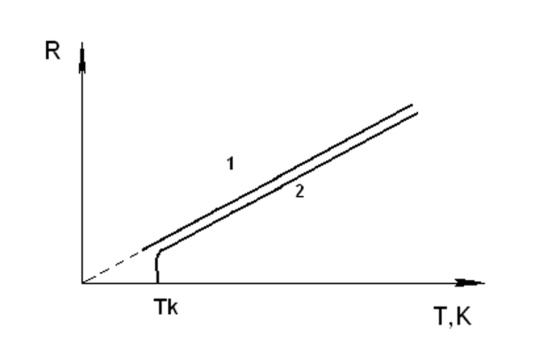Удельная электрическая проводимость 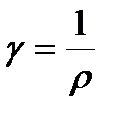, единица измерения - сименс на метр (См/м). Зависимость сопротивления от температуры ,

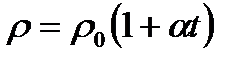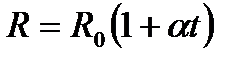
Работа тока 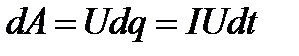или 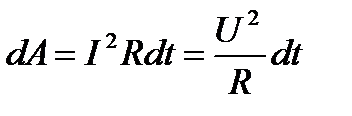Мощность тока 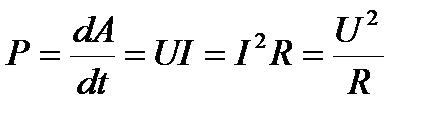Закон Джоуля-Ленца 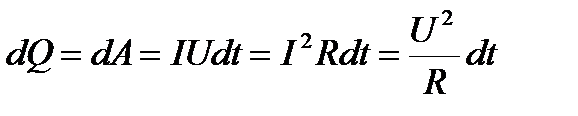или 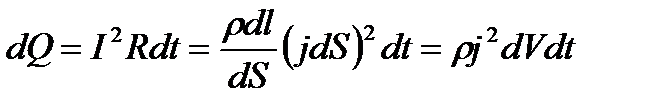Удельная тепловая мощность тока - количество теплоты, выделяющее за единицу времени в единице объема. 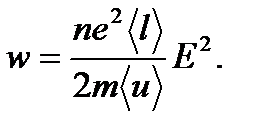Закон Джоуля-Ленца в дифференциальной форме 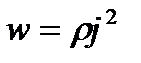или 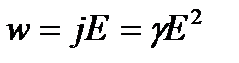Закон Ома для неоднородного участка цепи в интегральной форме (обобщенный закон Ома) 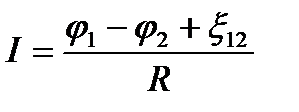Для замкнутой цепи 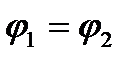; тогда 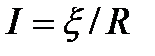, или 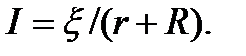, если r-внутреннее сопротивление источника тока, R - сопротивление внешней цепи. Для разомкнутой цепи 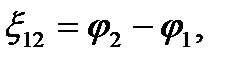Чтобы найти ЭДС источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

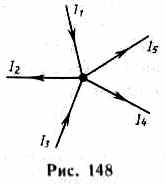
Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. Ток, входящий в узел, считается положительным, а ток, выходящий из узла - отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю 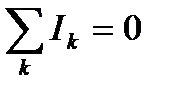Например, для рис.: 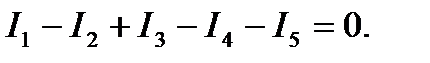Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Второе правило Кирхгофа получается из обобщенного закона Ома для разветвленных цепей.

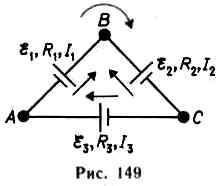
Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов 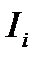на сопротивления 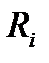соответствующих участков этого контура равна алгебраической сумме ЭДС 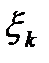, встречающихся в этом контуре 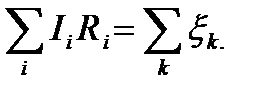При расчете сложных цепей постоян­ного тока необходимо:

1. Выбрать произвольное направление токов на всех участках цепи; действитель­ное направление токов определяется при решении задачи: если искомый ток полу­чится положительным, то его направление было выбрано правильно, отрицатель­ным — его истинное направление противо­положно выбранному.

2. Выбрать направление обхода кон­тура и строго его придерживаться; про­изведение IR положительно, если ток на данном участке совпадает с направлением обхода, и наоборот, ЭДС, действующие по выбранному направлению обхода, счита­ются положительными, против — отрица­тельными.

3. Составить столько уравнений, что­бы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рас­сматриваемой цепи); каждый рассматри­ваемый контур должен содержать хотя бы один элемент, не содержащийся в преды­дущих контурах, иначе получатся уравне­ния, являющиеся простой комбинацией уже составленных.